こんにちは、データサイエンスチーム tmtkです。
この記事では、スペクトラルクラスタリング（Spectral Clustering）について説明します。スペクトラルクラスタリングについて、具体的には、

• スペクトラルクラスタリングとは
• 行列の固有値分解によるグラフの連結成分分解の説明
• スペクトラルクラスタリングのアルゴリズムと計算例
• 関連する話題

を説明します。

スペクトラルクラスタリングとは

スペクトラルクラスタリングとは、クラスタリングアルゴリズムの一つです。クラスタリングは機械学習の方法のうち、教師なし学習に分類されます。データが与えられたとき、正解データなしでデータを複数の集団に分ける方法です。
スペクトラルクラスタリングの特徴は、データからグラフを生成し、グラフの連結成分分解を応用してクラスタリングするところです。クラスタリングアルゴリズムとして古典的なものに、KMeansやGaussian mixture modelがあります。KMeansやGaussian mixture modelはクラスタの中心点からの距離に基づいてクラスタリングを行いますが、スペクトラルクラスタリングでは連結性に注目してクラスタリングを行うため、KMeansやGaussian mixtureではうまくクラスタリングできなかったようなデータをうまくクラスタリングできることがあります。

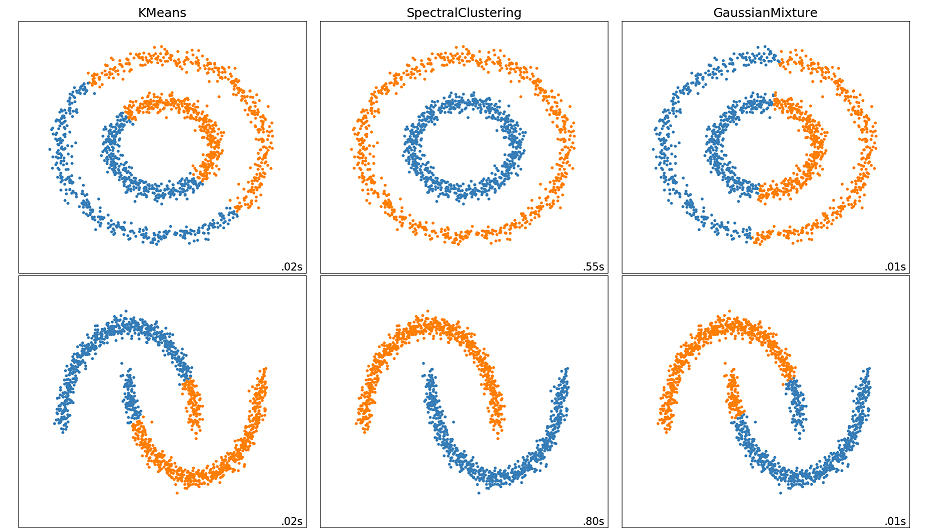
（KMeans, Spectral Clustering, Gaussian Mixtureの比較。画像はscikit-learnのページのプログラムを改変して作成しました。）

【事例集】AIや機械学習によるビッグデータ活用をしたい方にオススメ！

＜データ分析・機械学習の事例集＞
「AIによるキャスト評価システムの構築」「データ分析基盤の運用費用9割削減」など、AWSを利用したAI、機械学習の成功事例をご紹介します。

データ分析・機械学習の事例集をダウンロード

行列の固有値問題によるグラフの連結成分分解

スペクトラルクラスタリングのアルゴリズムを説明する前に、その基礎として、行列の固有値問題によってグラフの連結成分分解を行う方法を説明します。
いま、正の重みつき無向グラフ[latex]G=(V = \{ v_1, \ldots, v_n\}, E)[/latex]があるとします。その隣接行列を[latex]W=(w_{ij})[/latex]とします。ここで、[latex]w_{ij}[/latex]は[latex]w_{ij}=w_{ji}, w_{ii} =0, w_{ij}\geq 0[/latex]であり、[latex]w_{ij}[/latex]の値が大きいほど頂点[latex]i, j[/latex]が近いようにします。
たとえば、頂点1と頂点2が重み100の辺でつながっていて、頂点3と頂点4が重み20の辺でつながっているグラフ[latex]G_1[/latex]の場合、

隣接行列[latex]W[/latex]は
[latex]W=\left(\begin{array}{cccc}0 & 100 & 0 & 0\\100 & 0 & 0 & 0 \\0 & 0 & 0 & 20\\ 0 & 0 & 20 & 0\end{array}\right)[/latex]
になります。
隣接行列[latex]W=(w_{ij})[/latex]に対して、そのdegree matrixを
[latex]D=\left(\begin{array}{ccc}\sum_{j=1}^n w_{1j} & 0 & 0 \\0 & \ddots & 0 \\0 & 0 & \sum_{j=1}^n w_{nj}\end{array}\right)[/latex]
で定義します。グラフ[latex]G[/latex]のunnormalized graph Laplacianを
[latex]L=D-W[/latex]
で定義します。
グラフ[latex]G_1[/latex]の場合、degree matrix [latex]D[/latex]とunnormalized graph Laplacian [latex]L[/latex]は
[latex]D = \left(\begin{array}{cccc}100 & 0 & 0 & 0\\0 & 100 & 0 & 0 \\0 & 0 & 20 & 0\\ 0 & 0 & 0 & 20\end{array}\right) ,\, L=\left(\begin{array}{cccc}100 & -100 & 0 & 0\\-100 & 100 & 0 & 0 \\0 & 0 & 20 & -20\\ 0 & 0 & -20 & 20\end{array}\right)[/latex]
になります。
このとき、次の定理が成り立ちます。

定理

グラフ[latex]G=(V = \{ v_1, \ldots, v_n\}, E)[/latex]が[latex]K[/latex]個の連結成分をもち、[latex]V=\{v_1,\ldots,v_{c_1}\}\cup\{v_{c_1+1},\ldots,v_{c_2}\}\cup\cdots\cup\{v_{c_{K-1}+1},\ldots,v_n\}[/latex]と連結成分分解されるとする。このとき、[latex]G[/latex]のunnormalized graph Laplacian[latex]L[/latex]の固有値はすべて非負の実数である。また、固有値[latex]0[/latex]に対応する固有空間は、[latex](1,\ldots,\stackrel{c_1}{\stackrel{\vee}{1}},0,\ldots,0)^\mathrm{T},(0,\ldots,\stackrel{c_1}{\stackrel{\vee}{0}},\stackrel{c_1+1}{\stackrel{\vee}{1}},\ldots,\stackrel{c_2}{\stackrel{\vee}{1}},0,\ldots,0)^\mathrm{T},\ldots,(0,\ldots,0,,\stackrel{c_{K-1}+1}{\stackrel{\vee}{1}},\ldots,1)^\mathrm{T}[/latex]を基底にもつ。

証明

線形代数からわかります。詳細は参考文献を参照していただくとして、ここでは証明の概略を説明します。
まず、具体的に計算すると、対称行列[latex]L[/latex]は半正定値行列であることがわかります。また、グラフ[latex]G[/latex]が連結である場合、[latex]L[/latex]の固有値0に属する固有ベクトルは[latex](1, \ldots, 1)^\mathrm{T}[/latex]（とそのスカラー倍）のみであることがわかります。グラフが非連結である場合は、グラフの連結成分分解に対応して[latex]L[/latex]が線形写像として直和分解されるので、結論を得ます。
この定理を前の例で計算してみましょう。
[latex]x=\left(\begin{array}{c}x_1 \\x_2 \\x_3 \\x_4\end{array}\right)[/latex]
が[latex]L[/latex]の固有値[latex]0[/latex]に属する固有ベクトルだとすると、
[latex]Lx=0x[/latex]
すなわち、
[latex]\left(\begin{array}{cc}100x_1 & -100x_2 \\-100x_1 &+100x_2 \\20x_3& -20x_4 \\-20x_3& +20x_4 \end{array}\right)=0[/latex]
が成り立ちます。このことから、固有値0に属する固有空間は[latex](1,1,0,0)^\mathrm{T},(0,0,1,1)^\mathrm{T}[/latex]を基底にもつことがわかります。（ただし、基底の与え方は一意ではなく、たとえば[latex](1,1,1,1)^\mathrm{T}, (1,1,0,0)^\mathrm{T}[/latex]も別の基底になっていることに注意します。）
ここから、グラフの連結成分分解を得るには次のようにします。まず、この基底を並べて行列
[latex]U=\left(\begin{array}{cc}1& 0\\1&0\\0&1\\0&1\end{array}\right)[/latex]
をつくります。この行列を構成する行ベクトルをそれぞれ見ると、1行目と2行目がどちらも[latex](1, 0)[/latex]で同じで、3行目と4行目がどちらも[latex](0, 1)[/latex]で同じです。これはグラフの連結成分分解が[latex]\{v_1, v_2\}, \{v_3, v_4\}[/latex]で与えられることと対応しています。
このようにして、グラフの連結成分を、行列の固有値問題を解くことによって得ることができます。
以上の議論をまとめると、以下の手順によって、グラフの連結成分分解ができることがわかります。

1. グラフから隣接行列表現[latex]W[/latex]、degree matrix[latex]D[/latex]を計算し、unnormalized graph Laplacian[latex]L[/latex]を計算する。
2. unnormalized graph Laplacian[latex]L[/latex]の固有値0に属する固有空間の基底[latex]u_1, \ldots, u_K[/latex]を計算する。
3. 基底ベクトルを並べて行列[latex]U=(u_1 u_2 \cdots u_K)[/latex]を作る。
4. 行列[latex]U[/latex]のi行目とj行目の行ベクトルが等しければ、頂点[latex]v_i[/latex]と[latex]v_j[/latex]は同じ連結成分に属し、さもなくば違う連結成分に属している。

AWSのビッグデータ活用・機械学習導入支援サービス

スペクトラルクラスタリングのアルゴリズムと計算例

スペクトラルクラスタリングのアルゴリズムは、上に説明したグラフの連結成分分解を応用したものです。具体的には、以下のようなアルゴリズムで行います。
いま、クラスタ数[latex]K[/latex]が与えられているとします。

1. データからグラフを構築する。
2. グラフから隣接行列表現[latex]W[/latex]、degree matrix[latex]D[/latex]を計算し、unnormalized graph Laplacian[latex]L[/latex]を計算する。
3. unnormalized graph Laplacian[latex]L[/latex]の固有値が小さい順に固有ベクトルを[latex]K[/latex]個[latex]u_1, \ldots, u_K[/latex]を計算する。
4. 固有ベクトルを並べて行列[latex]U=(u_1 u_2 \cdots u_K)[/latex]を作る。
5. 行列[latex]U[/latex]の行ベクトルをK-meansなどを用いて[latex]K[/latex]個にクラスタリングする。
6. K-meansの結果、i行目が入ったクラスタを頂点[latex]v_i[/latex]の入るクラスタとする。

連結成分分解との相違点は、データからグラフを構築するステップが必要であるところと、連結成分分解のようにi行目とj行目が厳密に等しかったり異なったりしないために、K-meansなどを使う必要があるところです。
具体的に計算をしてみましょう。前のグラフとは少し変えて、次の連結なグラフを考えます。このグラフを[latex]K=2[/latex]個のクラスタに分類してみます。

このグラフのunnormalized graph Laplacianは
[latex]L=D-W =\left(\begin{array}{cccc}100&&&\\&101&&\\&&21&\\&&&20\end{array}\right)-\left(\begin{array}{cccc}0&100&&\\100&0&1&\\&1&0&20\\&&20&0\end{array}\right)=\left(\begin{array}{cccc}100&-100&&\\-100&101&-1&\\&-1&21&-20\\&&-20&20\end{array}\right)[/latex]
と計算でき、コンピュータを用いて計算すると、その固有値は
[latex]-1.15040601\times 10^{-14}, 0.984903474, 40.5110121, 200.504084[/latex]
で、対応する固有ベクトルは、有効数字2桁で四捨五入すると、
[latex]u_1 = \left(\begin{array}{c}1 \\1 \\1 \\1\end{array}\right), \, u_2 = \left(\begin{array}{c}1 \\ 0.99\\ -0.97\\ -1.0\end{array}\right), u_3 = \left(\begin{array}{c}1 \\ 0.59\\ -64\\ 62\end{array}\right), \, u_4 = \left(\begin{array}{c}1\\ -1.0\\ 0.0057\\ -0.00063\end{array}\right)[/latex]
です。固有値の小さいほうから固有ベクトルを[latex]K=2[/latex]つとり、並べると、
[latex]U = \left( \begin{array}{cc}1&1\\ 1&0.99\\1&-0.97\\1&-1.0\end{array}\right)[/latex]
この4つの行ベクトルをK-meansでクラスタリングしたら、1行目と2行目の[latex](1,1), (1, 0.99)[/latex]のクラスタと3行目と4行目の[latex](1, -0.97), (1, -1.0)[/latex]のクラスタに分かれることが予想できます。これは[latex]v_1, v_2[/latex]と[latex]v_3, v_4[/latex]にクラスタリングされることに対応しています。
同様に、[latex]K=3[/latex]で計算すると、固有値の小さいほうから固有ベクトルを[latex]K=3[/latex]個とって、
[latex]U = \left( \begin{array}{ccc}1&1&1\\ 1&0.99&0.59\\1&-0.97&-64\\1&-1.0&62\end{array}\right)[/latex]
の4つ行ベクトルを3クラスタにK-Meansでクラスタリングすることになります。この場合は[latex](1,1,1), (1,0.99,0.59)[/latex]のクラスタと[latex](1,-0.97, -64)[/latex]のクラスタと[latex](1, -1.0, 62)[/latex]のクラスタに分かれます。これは[latex]v_1, v_2[/latex]と[latex]v_3[/latex]と[latex]v_4[/latex]にクラスタリングされるということで、4つの頂点の中で[latex]v_1, v_2[/latex]の組み合わせが一番近くにあることに対応しています。

（よく見ると2点[latex](1, 1, 1)[/latex]と[latex](1, 0.99, 0.59)[/latex]が重なっています。）

関連する話題

スペクトラルクラスタリングではまずデータをグラフに変換します。グラフへの変換の仕方はいろいろあり、

• ε近傍法
• k近傍法
• 全結合法

などがあるようです。ユークリッド空間上の距離関数を[latex]d[/latex]とすると、データ[latex]x_1, x_2[/latex]の間の辺の重みは[latex]\exp(-d(x_1, x_2)^2/2\sigma^2)[/latex]などで与えることができます。さらに、行列を疎にするためのε近傍法やk近傍法などを用いるとよい、ということのようです。
また、graph Laplacian [latex]L[/latex]にはいろいろな亜種があり、
[latex]L_{sym} = D^{-1/2}LD^{1/2}[/latex]
や
[latex]L_{rw} = D^{-1}L[/latex]
などが使われるようです。どちらも [latex]L[/latex] と似た性質を持ちます。

まとめ

• グラフの連結成分分解を、行列の固有値問題に還元することができます。
• 固有値問題による連結成分分解を応用したクラスタリングが、スペクトラルクラスタリングです。

【事例集】AIや機械学習によるビッグデータ活用をしたい方にオススメ！

＜データ分析・機械学習の事例集＞
「AIによるキャスト評価システムの構築」「データ分析基盤の運用費用9割削減」など、AWSを利用したAI、機械学習の成功事例をご紹介します。

データ分析・機械学習の事例集をダウンロード

参考文献

• A Tutorial on Spectral Clusteringがこの分野のテキストの決定版のようです。本記事もこの資料を大いに参考にしています。
• Comparing different clustering algorithms on toy datasets – scikit-learn documentationクラスタリングアルゴリズムを比較する画像が面白いです。