こんにちは。データサイエンスチーム　山川です。
この記事はNHN テコラス Advent Calendar 2018の20日目の記事です。

はじめに

最近、因果推論に関する読書会を始めました。第二回目が数日後にあるので、ご興味のある方はお越しください。

さて、読書会で扱っているRによる実証分析 ―回帰分析から因果分析へ― は初心者向けで古典的な手法を扱っている本です。他方でもっと現代的な手法について、何人かでワークショップをやっています。私はその中で、LiNGAMという手法を担当しています。LiNGAMは例えばスライド「構造方程式モデルによる因果推論: 因果構造探索に関する最近の発展」の65ページ以降が詳しくて、相関ではなくて因果関係を推測する有力な手法の一つです。

講談社機械学習プロフェッショナルシリーズの「統計的因果探索」は国内で数少ないLiNGAMについての本ですが、残念ながらすぐ動かせるコードが有りません。そこで、以下でRでLiNGAMモデルを動かしてみます。

ちなみに、LiNGAMは linear non-Gaussian acyclic modelの略で、日本語に訳すと「線形非ガウス型非巡回モデル」といったところでしょう。実務者としては、

• モデルが識別可能である
• パス図を事前に推測しなくても、モデル推論ができる

といったありがたい特徴があります。

事前準備

まず必要なライブラリーをインストールします。RでLiNGAMを実行するためのpcalgというパッケージはBioconductorというCRAN外のサイトにあるパッケージに依存しているので、そのケアも必要です。なお、Rのバージョンが3.5.0未満の場合はこの手順ではインストールできませんのでお気をつけください。

install.packages("tidyverse")
install.packages("ggExtra") 
install.packages("BiocManager")
BiocManager::install(c("graph", "RBGL"))
install.packages("pcalg")

主たるパッケージを読み込みます。

library(tidyverse)
library(pcalg)

次に、分析用のデータフレームを4つ作成します。

df名	x1	x2	e1,e2の分布
df12g	e1	0.8 * x1 + e2	平均0, 分散1のガウス分布
df21g	0.8 * x2 + e1	e2	平均0, 分散1のガウス分布
df12n	e1	0.8 * x1 + e2	平均0, 分散1の一様分布
df21n	0.8 * x2 + e1	e2	平均0, 分散1の一様分布

ちなみに、最小値a, 最大値bの一様分布は

平均 =
分散 =

なので、平均0, 分散1のときはa = -sqrt(3), b = sqrt(3)となります

N <- 1000
set.seed(1234)
df12g <- data.frame(x1 = rnorm(N, mean = 0, sd = 1)) %>%
mutate(x2 = 0.8 * x1 + rnorm(N, mean = 0, sd = 1))
df21g <- data.frame(x2 = rnorm(N, mean = 0, sd = 1)) %>%
mutate(x1 = 0.8 * x2 + rnorm(N, mean = 0, sd = 1)) %>%
select(x1, x2)
df12n <- data.frame(x1 = runif(N, min = -1, max = 1) * sqrt(3)) %>%
mutate(x2 = 0.8 * x1 + runif(N, min = -1, max = 1) * sqrt(3))
df21n <- data.frame(x2 = runif(N, min = -1, max = 1) * sqrt(3)) %>%
mutate(x1 = 0.8 * x2 + runif(N, min = -1, max = 1) * sqrt(3)) %>%
select(x1, x2)

散布図で確認します。

plot_func <- function(df){ df %>% ggplot(aes(x1, x2)) + geom_point() +
xlim(c(-4, 4)) + ylim(c(-4, 4))
}
g12g <- plot_func(df12g)
g21g <- plot_func(df21g)
g12n <- plot_func(df12n)
g21n <- plot_func(df21n)
gridExtra::grid.arrange(g12g, g12n, g21g, g21n, nrow=2)

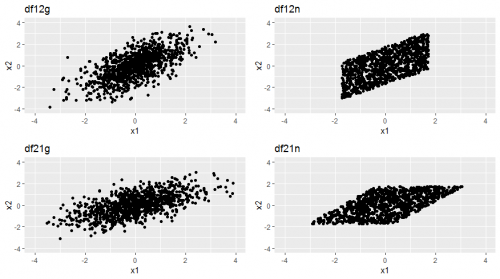
e1, e2がガウス分布に従うdf12g, df21gは、観測変数の分布が似ているため(書籍では「分布が同じ」と書かれています)、原因と結果の識別は困難です。

e1, e2が一様分布に従うdf12n, df21nの方は、因果方向の異なるモデルの観測変数の分布が異なるため、上手く因果推論ができると期待されます。

LiNGAMをやってみる

pcaglパッケージを読み込んでいれば、データフレームをLiNGAM関数に食わせるだけです。

model_12g <- lingam(df12g)
model_21g <- lingam(df21g)
model_12n <- lingam(df12n)
model_21n <- lingam(df21n)

とはいえ、これでは何もわからないので、まず因果グラフ（の隣接行列）を出力します。

as(model_12g, "amat")
as(model_21g, "amat")
as(model_12n, "amat")
as(model_21n, "amat")

Adjacency Matrix ‘amat’ (2 x 2) of type ‘pag’:
[,1] [,2]
[1,] . TRUE
[2,] . .
Adjacency Matrix ‘amat’ (2 x 2) of type ‘pag’:
[,1] [,2]
[1,] . .
[2,] TRUE .
Adjacency Matrix ‘amat’ (2 x 2) of type ‘pag’:
[,1] [,2]
[1,] . TRUE
[2,] . .
Adjacency Matrix ‘amat’ (2 x 2) of type ‘pag’:
[,1] [,2]
[1,] . .
[2,] TRUE .

わかりにくい出力ですが、

• 2×2の行列の[1,2]成分のみTRUEの場合はx1 –> x2
• 2×2の行列の[2,1]成分のみTRUEの場合はx2 –> x1

という因果関係を意味します。。つまり、

model_12gとmodel_12nはx1 –> x2

model_21gとmodel_21nはx2 –> x1

という因果関係が示唆されたということです。e1, e2が一様分布であるdf12n, df21nは正しく識別できていますが、それに加えてガウス分布であるdf12g, df21gも正しく識別できています。

次に、定数項の推測をします。

model_12g$ci
model_21g$ci
model_12n$ci
model_21n$ci

[1] -0.02659720 0.01177084
[1] -0.008342839 0.028951145
[1] 0.00400295 -0.01986628
[1] 0.005940824 0.054756518

真値は0なので、そこそこの精度と言えそうです。

最後に残差誤差の標準偏差の推測値を見ます。

model_12g$stde
model_21g$stde
model_12n$stde
model_21n$stde

[1] 0.9911724 0.9683295
[1] 0.9852158 1.0081611
[1] 0.9788190 0.9896831
[1] 0.9757174 0.9733218

真値は1なので、いずれも推測できています。

誤差がガウス分布に従うケースでも、正しく推測できていますが、どうもこれは「たまたま」だったようです。最初にデータフレームを作る際にset.seed(1234)と指定していますが、ここの値を変更すると、結果が変わることがありました。

1000回やってみる

ランダムシードの値を1234×1, 2, 3, … , 1000の1000とおりで同様の推測を実行してみました。

コードは長くなるので省略しますが、結果は

df名	x1 –> x2	x2 –> x1
df12g	339	661
df21g	668	332
df12n	1000	0
df21n	0	1000

でした。

df12gに関して標準偏差の推測値は

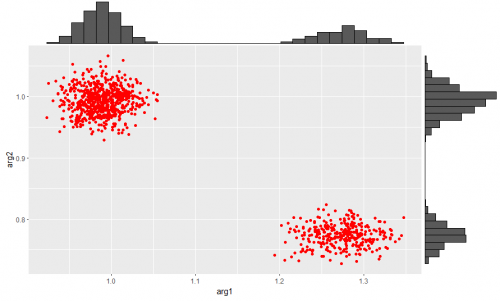
と、約3分の1が真値から大きく外れていますが、
df12nの方は

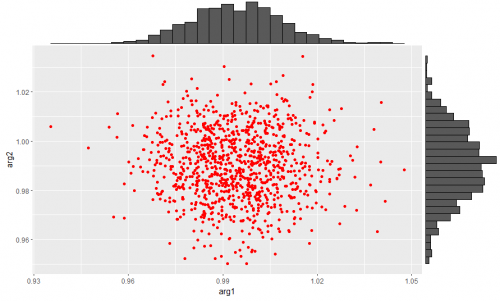
と真値から大きくずれていません。

最後に

2変数間の因果推論という最も簡単なケースでしたが、一様分布の場合は100%の識別性を実現できました。
実務的には変数の数はもっと多いので、組み合わせ爆発のリスクが伴います。それをどう解決するかは別のテーマになります。

また、書籍ではベイズ的アプローチや、時系列データの扱い、未観測な共通原因がある場合などさまざまな手法が紹介されていますので、ぜひ原典をあたってみてください。