Rで実践!欠損データ分析入門【1】
こんにちは。データサイエンスチームの t2sy です。
この記事は DataScience by DATAHOTEL tech blog Advent Calendar 2017 の8日目の記事です。
2回に渡り、欠損データの可視化・検定・代入に関するCRANパッケージをご紹介します。
今回、ご紹介するCRANパッケージは以下になります。
- VIM
- BaylorEdPsych
- imputeMissings
- mice
実行環境は R 3.3.2 です。
例として米国ボストン市郊外における地域別の住宅価格のデータセットである BostonHousing を扱います。BostonHousing データセットには以下のカラムがあります。
- crim: 人口1人当たりの犯罪発生率
- zn: 25,000 平方フィート以上の住居区画の占める割合
- indus: 小売業以外のビジネスが占める面積の割合
- chas: チャールズ川の周辺かを表すダミー変数 (1:yes 0: no)
- nox: 窒素酸化物濃度 (0.1ppm単位)
- rm: 住居あたりの平均部屋数
- age: 1940年以前から所有されている物件の割合
- dis: ボストン市内5箇所の雇用施設からの重み付けされた距離
- rad: 高速道路へのアクセス性を表す指標
- tax: $10,000あたりの不動産税率
- ptratio: 小学校教員一人あたりに対する児童の人数
- b: Bを街ごとの黒人の比率として 1000(B-0.63)^2
- lstat: 階級が低い層の人口に占める割合
- medv: 持家価格の中央値 ($1,000単位)
R で BostonHousing データセットを読み込んで、まずデータの要約を確認します。
> data(BostonHousing, package = "mlbench")
> data <- BostonHousing
> summary(data)
crim zn indus chas nox
Min. : 0.00632 Min. : 0.00 Min. : 0.46 0:471 Min. :0.3850
1st Qu.: 0.08204 1st Qu.: 0.00 1st Qu.: 5.19 1: 35 1st Qu.:0.4490
Median : 0.25651 Median : 0.00 Median : 9.69 Median :0.5380
Mean : 3.61352 Mean : 11.36 Mean :11.14 Mean :0.5547
3rd Qu.: 3.67708 3rd Qu.: 12.50 3rd Qu.:18.10 3rd Qu.:0.6240
Max. :88.97620 Max. :100.00 Max. :27.74 Max. :0.8710
rm age dis rad
Min. :3.561 Min. : 2.90 Min. : 1.130 Min. : 1.000
1st Qu.:5.886 1st Qu.: 45.02 1st Qu.: 2.100 1st Qu.: 4.000
Median :6.208 Median : 77.50 Median : 3.207 Median : 5.000
Mean :6.285 Mean : 68.57 Mean : 3.795 Mean : 9.549
3rd Qu.:6.623 3rd Qu.: 94.08 3rd Qu.: 5.188 3rd Qu.:24.000
Max. :8.780 Max. :100.00 Max. :12.127 Max. :24.000
tax ptratio b lstat
Min. :187.0 Min. :12.60 Min. : 0.32 Min. : 1.73
1st Qu.:279.0 1st Qu.:17.40 1st Qu.:375.38 1st Qu.: 6.95
Median :330.0 Median :19.05 Median :391.44 Median :11.36
Mean :408.2 Mean :18.46 Mean :356.67 Mean :12.65
3rd Qu.:666.0 3rd Qu.:20.20 3rd Qu.:396.23 3rd Qu.:16.95
Max. :711.0 Max. :22.00 Max. :396.90 Max. :37.97
medv
Min. : 5.00
1st Qu.:17.02
Median :21.20
Mean :22.53
3rd Qu.:25.00
Max. :50.00
このデータには欠測値は含まれていません。このようなデータセットを完全データと言います。
欠測メカニズムの分類
欠損データの分析に入る前に欠測メカニズムの分類を簡単に整理します。欠損データは欠測メカニズムにより大きく3パターンに分類されます。
- MCAR (Missing Completely at Random): 完全にランダムに欠測している
- MAR (Missing at Random): ランダムな欠測。欠測するかしないかが観測値に依存するが欠測値には依存しない
- MNAR (Missing Not At Random): 欠測値に依存して欠測している
BostonHousing データセットを基に MCAR/MAR を仮定できるような欠損データを作成します。欠損データの作成には missForest::prodNA() を用いました。欠測値の割合を20%に設定しています。
> set.seed(123)
> data.mis <- missForest::prodNA(data, noNA = 0.2)
> summary(data.mis)
crim zn indus chas
Min. : 0.00632 Min. : 0.0 Min. : 0.46 0 :375
1st Qu.: 0.07438 1st Qu.: 0.0 1st Qu.: 5.13 1 : 24
Median : 0.24217 Median : 0.0 Median : 9.69 NA's:107
Mean : 3.45009 Mean : 11.1 Mean :11.16
3rd Qu.: 3.54343 3rd Qu.: 12.5 3rd Qu.:18.10
Max. :73.53410 Max. :100.0 Max. :27.74
NA's :98 NA's :108 NA's :93
nox rm age dis
Min. :0.3850 Min. :3.561 Min. : 6.60 Min. : 1.130
1st Qu.:0.4490 1st Qu.:5.886 1st Qu.: 46.83 1st Qu.: 2.075
Median :0.5380 Median :6.185 Median : 78.40 Median : 2.988
Mean :0.5562 Mean :6.273 Mean : 69.78 Mean : 3.697
3rd Qu.:0.6240 3rd Qu.:6.617 3rd Qu.: 94.08 3rd Qu.: 5.057
Max. :0.8710 Max. :8.725 Max. :100.00 Max. :12.127
NA's :105 NA's :107 NA's :128 NA's :87
rad tax ptratio b
Min. : 1.000 Min. :187.0 Min. :12.60 Min. : 0.32
1st Qu.: 4.000 1st Qu.:281.0 1st Qu.:16.90 1st Qu.:375.44
Median : 5.000 Median :330.0 Median :18.70 Median :391.34
Mean : 9.643 Mean :411.4 Mean :18.36 Mean :355.18
3rd Qu.:24.000 3rd Qu.:666.0 3rd Qu.:20.20 3rd Qu.:396.16
Max. :24.000 Max. :711.0 Max. :22.00 Max. :396.90
NA's :100 NA's :114 NA's :93 NA's :94
lstat medv
Min. : 1.73 Min. : 5.00
1st Qu.: 6.70 1st Qu.:17.05
Median :10.97 Median :21.40
Mean :12.39 Mean :22.81
3rd Qu.:16.56 3rd Qu.:26.30
Max. :36.98 Max. :50.00
NA's :91 NA's :91
欠損データの可視化
欠損データをうまく扱うためにも、まず欠測値の傾向を可視化してみます。
VIMパッケージを使うと各カラムごとの欠測値の割合や欠測パターンの組み合わせを確認できます。
> library(VIM)
>
> vim.aggr <- aggr(data.mis,
+ col = c('white','red'),
+ numbers = TRUE,
+ sortVars = FALSE,
+ prop = TRUE,
+ labels = names(data.mis),
+ cex.axis = .8,
+ gap = 3)
>
> vim.aggr
Missings in variables:
Variable Count
crim 98
zn 108
indus 93
chas 107
nox 105
rm 107
age 128
dis 87
rad 100
tax 114
ptratio 93
b 94
lstat 91
medv 91
カラムごとにややばらつきはありますが概ね2割程度の欠測があることが確認できます。また、欠測パターンの組み合わせを見ると特定の欠測パターンに大きく偏っている様子はなさそうです。

LittleのMCAR検定
欠測のランダム性を検定で確認してみます。LittleのMCAR検定はデータが MCAR または MAR であるという帰無仮説のもとで検定を行います。
Rでは BaylorEdPsych::LittleMCAR() でLittleのMCAR検定が行えます。
> library(BaylorEdPsych) > > test.mcar <- LittleMCAR(data.mis) > print(test.mcar$p.value) [1] 0.1895435
p値が 0.1895 と大きいことから、MCAR または MAR であるという帰無仮説は棄却されませんでした。
リストワイズ削除
欠損データの分析に入ります。元の完全データと欠損データからそれぞれ持家価格の中央値を目的変数とする線形回帰モデルを作ってみます。
ただし、欠損データではリストワイズ削除あるいは完全ケース分析と呼ばれる欠測値を含む行を削除してから分析を行う方法を取ります。
> model <- lm(medv ~ ., data = data) > summary(model) Call: lm(formula = medv ~ ., data = data) Residuals: Min 1Q Median 3Q Max -15.595 -2.730 -0.518 1.777 26.199 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 3.646e+01 5.103e+00 7.144 3.28e-12 *** crim -1.080e-01 3.286e-02 -3.287 0.001087 ** zn 4.642e-02 1.373e-02 3.382 0.000778 *** indus 2.056e-02 6.150e-02 0.334 0.738288 chas1 2.687e+00 8.616e-01 3.118 0.001925 ** nox -1.777e+01 3.820e+00 -4.651 4.25e-06 *** rm 3.810e+00 4.179e-01 9.116 < 2e-16 *** age 6.922e-04 1.321e-02 0.052 0.958229 dis -1.476e+00 1.995e-01 -7.398 6.01e-13 *** rad 3.060e-01 6.635e-02 4.613 5.07e-06 *** tax -1.233e-02 3.760e-03 -3.280 0.001112 ** ptratio -9.527e-01 1.308e-01 -7.283 1.31e-12 *** b 9.312e-03 2.686e-03 3.467 0.000573 *** lstat -5.248e-01 5.072e-02 -10.347 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 4.745 on 492 degrees of freedom Multiple R-squared: 0.7406, Adjusted R-squared: 0.7338 F-statistic: 108.1 on 13 and 492 DF, p-value: < 2.2e-16 > > model.mis <- lm(medv ~ ., data = data.mis, na.action = na.omit) > summary(model.mis) Call: lm(formula = medv ~ ., data = data.mis, na.action = na.omit) Residuals: Min 1Q Median 3Q Max -2.8694 -0.9296 0.1885 0.9823 3.1156 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -16.685878 16.050082 -1.040 0.32083 crim 0.098799 0.106068 0.931 0.37161 zn 0.074685 0.036201 2.063 0.06353 . indus 0.828146 0.216853 3.819 0.00285 ** chas1 1.371909 2.663485 0.515 0.61669 nox 20.522828 25.672194 0.799 0.44097 rm 6.372158 1.685456 3.781 0.00304 ** age -0.090948 0.042865 -2.122 0.05740 . dis -0.484441 0.505210 -0.959 0.35822 rad -0.522924 0.253772 -2.061 0.06380 . tax -0.011002 0.012063 -0.912 0.38132 ptratio -0.751385 0.320199 -2.347 0.03872 * b 0.029582 0.009374 3.156 0.00915 ** lstat -0.075170 0.156835 -0.479 0.64112 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 2.284 on 11 degrees of freedom (481 observations deleted due to missingness) Multiple R-squared: 0.9744, Adjusted R-squared: 0.9441 F-statistic: 32.15 on 13 and 11 DF, p-value: 7.576e-07
リストワイズ削除を行うことで標本サイズが元の5%以下となってしまい、分析結果も完全データの結果と大きく異なっています。今回のデータに対してリストワイズ削除を適用することは望ましくなさそうです。
代入法
欠測値に尤もらしい値を代入して擬似完全データを得る代入法を試してみます。今回は触れませんが、欠損データに対して最尤法を用いるアプローチもあります。
単一代入法
一つの欠測値に一つの値を代入する単一代入法 (single imputation) には以下のような方法があります。
- 代表値代入
- (確率的)回帰代入
- マッチング
- 時系列で最後に得られた値の代入 (LOCF/LVCF)
- 機械学習手法による代入
今回は imputeMissings::impute() で中央値を代入し、得られた擬似完全データに対して完全データと同様に線形回帰を行います。
> library(imputeMissings) > > data.comp.median <- impute(data.mis, method = "median/mode") > model.median <- lm(medv ~ ., data = data.comp.median) > summary(model.median) Call: lm(formula = medv ~ ., data = data.comp.median) Residuals: Min 1Q Median 3Q Max -17.659 -3.059 -0.582 2.165 28.285 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.239e+01 5.617e+00 3.986 7.73e-05 *** crim -2.837e-02 4.406e-02 -0.644 0.519880 zn 5.090e-03 1.517e-02 0.336 0.737317 indus -1.076e-01 6.153e-02 -1.749 0.080901 . chas1 3.395e+00 1.245e+00 2.727 0.006614 ** nox -1.249e+01 3.727e+00 -3.352 0.000864 *** rm 4.414e+00 4.995e-01 8.838 < 2e-16 *** age 1.125e-02 1.430e-02 0.787 0.431502 dis -5.913e-01 1.907e-01 -3.100 0.002044 ** rad 6.139e-02 4.935e-02 1.244 0.214059 tax -2.556e-04 2.630e-03 -0.097 0.922626 ptratio -9.649e-01 1.534e-01 -6.291 6.98e-10 *** b 1.031e-02 3.446e-03 2.992 0.002911 ** lstat -3.779e-01 5.565e-02 -6.791 3.23e-11 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 5.815 on 492 degrees of freedom Multiple R-squared: 0.5505, Adjusted R-squared: 0.5386 F-statistic: 46.35 on 13 and 492 DF, p-value: < 2.2e-16
age、nox 変数の分布を完全データ、欠損データ、擬似完全データで比較してみると中央値代入により分布が歪められていることがわかります。
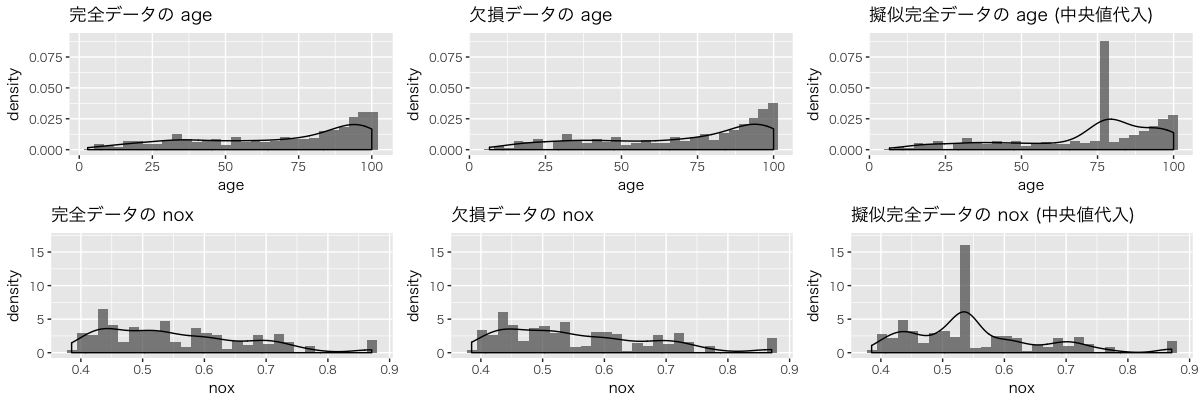
単一代入法では多くの場合、分散を過少推定をしてしまい、結果として標準誤差 (推定値の標準偏差) も過小評価してしまうことが知られています。
多重代入法
多重代入法 (multiple imputation; MI) は単一代入法を m (>1) 回繰り返し、得られた擬似完全データごとに計算した推定値を統合します。
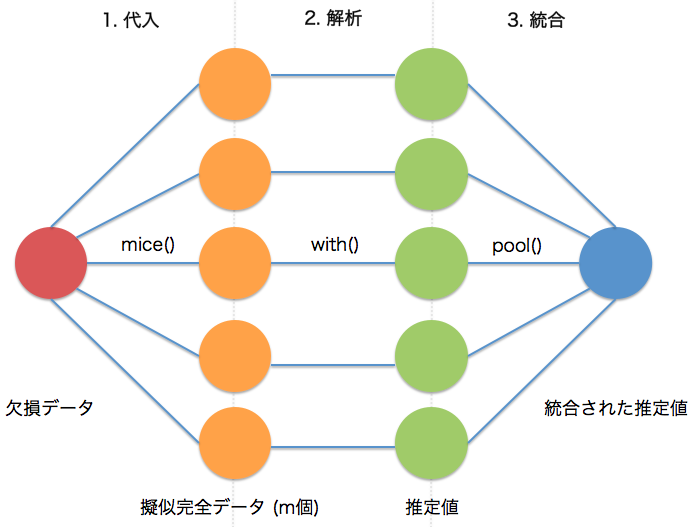
R で多重代入を行うパッケージを探したところいくつか見つかりました。
- Norm
- mi
- mice
- Amelia
- smcfcs
今回は多重代入法の中でも代表的な手法である連鎖式による多重代入法 (Multivariate Imputation by Chained Equations; MICE)をmiceパッケージを使って試してみます。
mice::mice() には擬似完全データの個数 m、代入法 method などを指定します。例えば m を 1、 method を mean にすると平均値代入による単一代入法となります。
今回は m を 10、 method を予測平均マッチング (predictive mean matching; pmm) としました。予測平均マッチングは回帰代入とマッチングを組み合わせた手法で回帰した値に近い観測値をランダムに選択し代入します。
> library(mice) > imp <- mice(data.mis, + m = 10, + maxit = 50, + method = "pmm", + printFlag = FALSE, + seed = 12345) > > summary(imp) Multiply imputed data set Call: mice(data = data.mis, m = 10, method = "pmm", maxit = 50, printFlag = FALSE, seed = 12345) Number of multiple imputations: 10 Missing cells per column: crim zn indus chas nox rm age dis rad 98 108 93 107 105 107 128 87 100 tax ptratio b lstat medv 114 93 94 91 91 Imputation methods: crim zn indus chas nox rm age dis rad "pmm" "pmm" "pmm" "pmm" "pmm" "pmm" "pmm" "pmm" "pmm" tax ptratio b lstat medv "pmm" "pmm" "pmm" "pmm" "pmm" VisitSequence: crim zn indus chas nox rm age dis rad 1 2 3 4 5 6 7 8 9 tax ptratio b lstat medv 10 11 12 13 14 PredictorMatrix: crim zn indus chas nox rm age dis rad tax ptratio b lstat medv crim 0 1 1 1 1 1 1 1 1 1 1 1 1 1 zn 1 0 1 1 1 1 1 1 1 1 1 1 1 1 indus 1 1 0 1 1 1 1 1 1 1 1 1 1 1 chas 1 1 1 0 1 1 1 1 1 1 1 1 1 1 nox 1 1 1 1 0 1 1 1 1 1 1 1 1 1 rm 1 1 1 1 1 0 1 1 1 1 1 1 1 1 age 1 1 1 1 1 1 0 1 1 1 1 1 1 1 dis 1 1 1 1 1 1 1 0 1 1 1 1 1 1 rad 1 1 1 1 1 1 1 1 0 1 1 1 1 1 tax 1 1 1 1 1 1 1 1 1 0 1 1 1 1 ptratio 1 1 1 1 1 1 1 1 1 1 0 1 1 1 b 1 1 1 1 1 1 1 1 1 1 1 0 1 1 lstat 1 1 1 1 1 1 1 1 1 1 1 1 0 1 medv 1 1 1 1 1 1 1 1 1 1 1 1 1 0 Random generator seed value: 12345 > > data.comp.mice <- complete(imp, "long")
m 個の擬似完全データから m = 1 の結果を取り出し、先ほどの中央値代入と同様に age、nox 変数の分布で比較してみます。今回のデータに対しては予測平均マッチングによる代入は中央値代入より精度の良い代入と言えそうです。
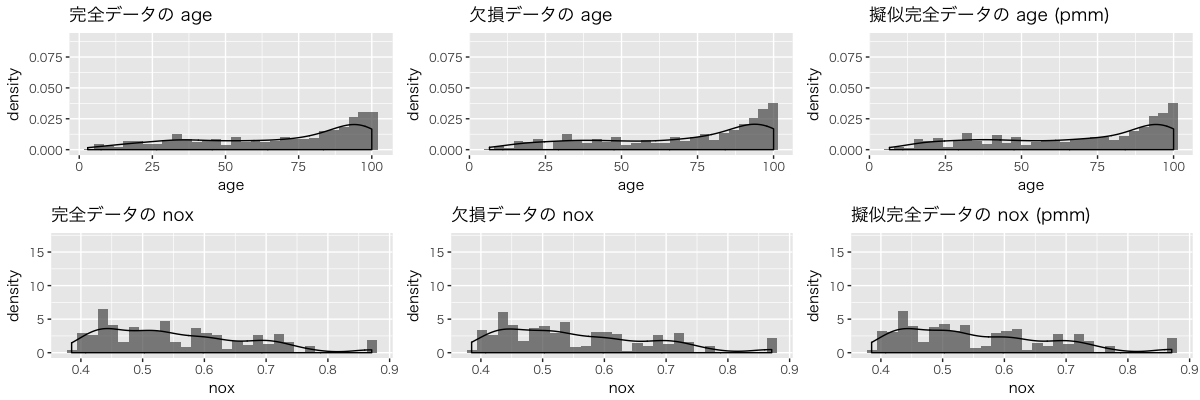
mice::densityplot() で各変数の分布を確認できます。
> densityplot(imp)
青線が欠損データ、 赤線が m 個の擬似完全データの分布です。

次に、得られた m 個の擬似完全データからパラメータを推定し統合します。
以下では、m 回の代入結果を含む mids S3オブジェクトを with() に渡し、m 個の線形回帰モデルを構築し、最後に mise::pool() により Rubin’s Rule を利用した推定値の統合を行っています。 MICE や Rubin’s Rule の詳細については参考文献をご参照ください。
> library(magrittr) > combine <- imp %>% + with(lm(medv ~ crim + zn + indus + chas + nox + rm + age + dis + rad + tax + ptratio + b + lstat)) %>% + pool() > summary(combine) est se t df Pr(>|t|) (Intercept) 50.206560402 8.953733099 5.6073327 19.27730 1.978599e-05 crim -0.052572694 0.045363654 -1.1589167 100.01301 2.492498e-01 zn 0.044198734 0.024181164 1.8278166 19.62945 8.281857e-02 indus -0.025879125 0.077477783 -0.3340199 48.05632 7.398178e-01 chas2 4.757208579 1.183639373 4.0191368 52.83613 1.862649e-04 nox -26.761262852 7.130894253 -3.7528621 16.69243 1.629058e-03 rm 3.336703725 0.609137436 5.4777519 31.03988 5.435545e-06 age 0.019242630 0.021510674 0.8945620 23.21064 3.802043e-01 dis -1.437235786 0.281557930 -5.1045829 36.80417 1.033835e-05 rad 0.336697276 0.120136069 2.8026327 16.26657 1.262201e-02 tax -0.009941573 0.006135206 -1.6204139 18.95884 1.216574e-01 ptratio -1.315557832 0.165442579 -7.9517488 49.05728 2.246519e-10 b 0.004913386 0.003506306 1.4012996 61.48859 1.661518e-01 lstat -0.518529168 0.066703355 -7.7736595 47.23488 5.379048e-10 lo 95 hi 95 nmis fmi lambda (Intercept) 31.484410964 68.928709839 NA 0.6763048 0.6443780 crim -0.142572749 0.037427360 98 0.2700228 0.2555697 zn -0.006303402 0.094700871 108 0.6704528 0.6385036 indus -0.181653933 0.129895683 93 0.4197234 0.3960659 chas2 2.382956756 7.131460403 NA 0.3977810 0.3754087 nox -41.827279611 -11.695246093 105 0.7236624 0.6924244 rm 2.094424427 4.578983022 107 0.5321880 0.5029862 age -0.025233254 0.063718514 128 0.6175849 0.5859943 dis -2.007828821 -0.866642751 87 0.4860926 0.4589048 rad 0.082358957 0.591035595 100 0.7322909 0.7012819 tax -0.022784593 0.002901448 114 0.6817121 0.6498177 ptratio -1.648017322 -0.983098342 93 0.4148814 0.3915034 b -0.002096781 0.011923552 94 0.3643902 0.3440469 lstat -0.652701398 -0.384356938 91 0.4238039 0.3999127
最後に完全データのパラメータ推定値とMICEによる擬似完全データのパラメータ推定値を比較してみます。ややずれているパラメータがいくつかありますが、今回のデータに対してはそこそこの精度で推定できていると思います。ただし、素直に Rubin’s Rule を用いた場合、推定量の分散に対してバイアスを持つことが指摘されている点には実際の分析では注意が必要です。
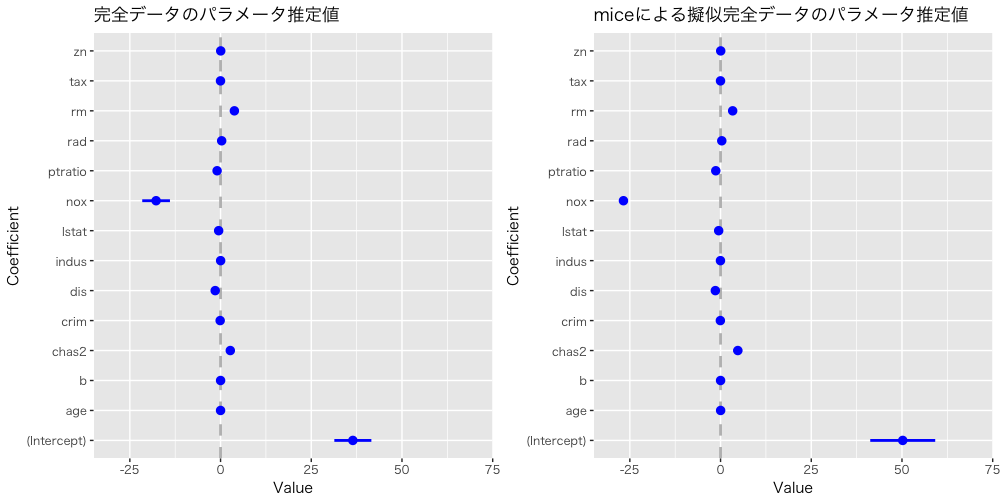
おわりに
今回はBostonHousingデータセットから欠損データを生成し、欠損データの可視化、MCAR検定、単一代入法と多重代入法による代入を R のコードを交えてご紹介しました。後半の Rで実践!欠損データの分析入門【2】 では機械学習手法を用いた欠損データの代入についてご紹介したいと思います。
参考文献
- Rubin, D.B. (1987). Multiple Imputation for Nonresponse in Surveys. New York: John Wiley and Sons.
- Little and Rubin. (2002). Statistical Analysis with Missing Data. Wiley.
- Stef van Buuren. (2011). mice: Multivariate Imputation by Chained Equations in R. Journal of Statistical Software.
テックブログ新着情報のほか、AWSやGoogle Cloudに関するお役立ち情報を配信中!
Follow @twitter2016年11月、データサイエンティストとして中途入社。時系列分析や異常検知、情報推薦に特に興味があります。クロスバイク、映画鑑賞、猫が好き。
Recommends
こちらもおすすめ
-

Rで実践!欠損データ分析入門【2】
2017.12.20
-

Pythonで時系列データをクラスタリングする方法
2017.12.12
-

うわさのMicrosoft 365 Businessをさわってみた
2017.12.20
-

k平均法による減色処理に混合ガウスモデルを適用してもうまくいかない
2017.12.25
Special Topics
注目記事はこちら

データ分析入門
これから始めるBigQuery基礎知識
2024.02.28

AWSの料金が 10 %割引になる!
『AWSの請求代行リセールサービス』
2024.07.16


