こんにちは。データサイエンスチームのtmtkです。
この記事では、ニューラルネットワークの機械学習における「宝くじ仮説（Lottery Ticket Hypothesis）」について、解説・実験します。

はじめに

「The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks（宝くじ仮説：訓練できる疎なニューラルネットワークを見つけること）」というJonathan Frankle氏とMichael Carbin氏による論文があります。この論文は2018年3月にarXivで公開され、2019年5月にはディープラーニングのカンファレンスであるICLR 2019でBest Paper Awardに選ばれました。
この論文では、「宝くじ仮説（The Lottery Ticket Hypothesis）」というニューラルネットワークに関する仮説が提唱され、仮説を支える実験がいくつか実行されています。また、宝くじ仮説をおしひろげて、「宝くじ予想（The Lottery Ticket Conjecture）」というものも提唱しています。
このブログ記事では、この論文の宝くじ仮説を紹介・解説するとともに、論文に記されている実験の一部を追試してみます。

宝くじ仮説とは

宝くじ仮説は、論文中に以下のように記されています。

The Lottery Ticket Hypothesis. A randomly-initialized, dense neural network contains a subnetwork that is initialized such that—when trained in isolation—it can match the test accuracy of the original network after training for at most the same number of iterations.

---

宝くじ仮説 ランダムに初期化された密なニューラルネットワークは、単独で高々同じイテレーション数だけ訓練すればテスト精度が元のネットワークに匹敵するまで上がるように初期化された部分ネットワークをもつ。
（拙訳）

この宝くじ仮説の言明中の「部分ネットワーク（subnetwork）」を宝くじにおける当たりくじにたとえて、宝くじ仮説という名前がつけられているのでしょう。
ニューラルネットワークの不要な重みを0にすることを刈り込み（pruning）といいますが、この論文は「Introduction」部によると刈り込みの研究を背景としてもつようです。

この論文の面白いところは、刈り込みで得られる部分ニューラルネットワークの構造そのものが単独で重要なわけではなく、刈り込みで得られた部分ネットワークと刈り込みに使われた初期値の両方が重要なのだという点だと思います。また、本記事では詳しく紹介しませんが、宝くじ予想がニューラルネットワークの学習の仕組みについての示唆を与えているところも面白い点だと思います。

実験

それでは、論文の2章「Winning Tickets in Fully-Connected Networks」で説明されている実験の一部を追試してみます。なお、論文での実験となるべく条件はそろえるようにしていますが、違いはいくつか残っていると思います。たとえば、論文では同じ実験を何度も繰り返して乱数によるばらつきを抑える工夫がされていますが、本記事では一度だけ実験を行います。また、論文では最終層への接続を刈り込む割合は他の半分にしていますが、この記事では他の層と同じ割合にしています。

論文によれば、「当たりくじ」を見つけるためには、刈り込みを繰り返して刈り込まれずに残った重みの部分を「当たりくじ」とみなすということです。
具体的には、以下のようにします。入力とパラメータをもつニューラルネットワークをとおきます。パラメータのランダムな初期値を一つとり、固定します。刈り込まれたネットワーク構造を表すマスクをパラメータと同じ形（shape）ですべての要素が1のものとして初期化します（マスクの各要素は0または1の値をとり、切断を0、接続を1で表すことで刈り込まれたネットワークの構造を表現します。すると、刈り込まれたネットワークのパラメータはアダマール積 をとることで表現できます）。重みを刈り込む割合と刈り込みの繰り返し回数と訓練のイテレーション数を決めておきます。以下の手順を回繰り返します。

1. ニューラルネットワークをマスクした初期値で初期化し、をえる
2. ニューラルネットワークをイテレーション訓練し、学習済みパラメータを得る
3. 学習済みパラメータの各要素でまだ刈り込まれていないもののうち、絶対値の小さいほうから個の重みを刈り込み、マスクを更新する
4. 新しく得られたマスクを使って1.に戻る

こうして得られたマスクが刈り込まれたニューラルネットワークの構造を表しています。

実際に、KerasとPython 3を使って実験してみましょう。実験には、GPUを有効にしたGoogle Colaboratoryを使用しています。
まずは必要なライブラリをimportします。

import numpy as np
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Flatten
from keras.optimizers import Adam
from keras.callbacks import Callback, EarlyStopping
from keras.preprocessing.image import ImageDataGenerator
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

データとしてはMNISTを使うため、準備します。

num_classes = 10

(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = np.expand_dims(x_train.astype('float32'), -1)
x_test = np.expand_dims(x_test.astype('float32'), -1)
x_train /= 255
x_test /= 255
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)

x_train, x_val, y_train, y_val = train_test_split(
    x_train, y_train, test_size=10000, stratify=y_train
)

ネットワークアーキテクチャとしては、28*28=784ユニットの入力層、300ユニットの全結合層、100ユニットの全結合層、10ユニットの全結合出力層というシンプルなアーキテクチャを使います。ネットワークを構築します。また、初期化されたパラメータを initial_weights として保存します。

def get_lenet():
    """Return a simple fully-connected model."""
    model = Sequential()
    model.add(Flatten(input_shape=(28, 28, 1)))
    model.add(Dense(300, activation='relu', kernel_initializer="glorot_normal"))
    model.add(Dense(100, activation='relu', kernel_initializer="glorot_normal"))
    model.add(Dense(num_classes, activation='softmax', kernel_initializer="glorot_normal"))

    model.compile(loss='categorical_crossentropy',
                  optimizer=Adam(lr=1.2e-3),
                  metrics=['accuracy'])
    return model

model = get_lenet()
initial_weights = [layer.get_weights() for layer in model.layers[1:]] # \theta_0
model.summary()

まずは通常のように学習します。なお、訓練時間の節約のため、元論文よりもイテレーション数を少なく、かついくつかのイテレーションをまとめて1エポックとしています。

batch_size = 60
# Change hyperparameters for the sake of time
steps_per_epoch = 100 # originally 1
iterations = 5000 # originally 50000
epochs = iterations // steps_per_epoch

datagen = ImageDataGenerator()

history = model.fit_generator(
    datagen.flow(x_train, y_train, batch_size=batch_size),
    steps_per_epoch=steps_per_epoch,
    epochs=epochs,
    validation_data=(x_val, y_val),
    verbose=0,
    callbacks=[EarlyStopping(patience=epochs, restore_best_weights=True)]
)

通常のように学習した場合の、早期終了のイテレーション数とそのときの精度を計算します。

loss, acc = model.evaluate(x_test, y_test, verbose=0)
print("Accuracy at Early-Stop:", acc)
print(
    "Early-Stop Iteration:",
    (np.argmin(np.array(history.history["val_loss"])) + 1) * steps_per_epoch
)

Accuracy at Early-Stop: 0.9792
Early-Stop Iteration: 4300

すると、4300イテレーション目で精度97.9%を達成していることがわかります。

ここで、刈り込みのため、重みをマスクでマスクする機能を作ります。今回はKerasのCallbackとして実現します。

class LeNetPruneCallback(Callback):
    """Neural Network Pruning Callback"""
    def __init__(self, masks):
        super().__init__()
        self.masks = masks
    def on_batch_end(self, batch, logs=None):
        weights = [layer.get_weights() for layer in self.model.layers[1:]]
        masked_weights = [
            (kernel_weight * mask, bias_weight)
            for (kernel_weight, bias_weight), mask
            in zip(weights, self.masks)
        ]
        for layer, weight in zip(self.model.layers[1:], masked_weights):
            layer.set_weights(weight)
    def on_batch_begin(self, batch, logs=None):
        weights = [layer.get_weights() for layer in self.model.layers[1:]]
        masked_weights = [
            (kernel_weight * mask, bias_weight)
            for (kernel_weight, bias_weight), mask
            in zip(weights, self.masks)]
        for layer, weight in zip(self.model.layers[1:], masked_weights):
            layer.set_weights(weight)

今回は重みを刈り込む割合を、刈り込みの繰り返し回数を回に設定します。最終的に、の重みが残ります。

prune_rate = 0.2 # p
prune_iteration_count = 10 # n
masks = [np.ones((784, 300)), np.ones((300, 100)), np.ones((100, 10))] # m

def prune_weight_mask(weight, prune_rate):
    """Create a new mask"""
    threshold = np.percentile(np.abs(weight), prune_rate * 100)
    return (np.abs(weight) > threshold).astype("float32")

for i in range(prune_iteration_count):
    for layer, initial_weight in zip(model.layers[1:], initial_weights):
        layer.set_weights(initial_weight)

    prune_rate_for_iteration = 1 - (1 - prune_rate) ** (i + 1)

    model.fit_generator(
        datagen.flow(x_train, y_train, batch_size=batch_size),
        steps_per_epoch=steps_per_epoch,
        epochs=epochs,
        validation_data=(x_val, y_val),
        verbose=0,
        callbacks=[
            LeNetPruneCallback(masks),
            EarlyStopping(patience=epochs, restore_best_weights=True)
        ]
    )
    kernel_weights = [layer.get_weights()[0] for layer in model.layers[1:]]
    masks = [
        prune_weight_mask(kernel_weight, prune_rate_for_iteration)
        for kernel_weight in kernel_weights
    ]

すると、変数 masks にマスクが入ります。こうして得られたネットワーク刈り込み済みネットワーク構造と、最初の初期値を使って、最初から訓練しなおします。

model = get_lenet()
for layer, weight in zip(model.layers[1:], initial_weights):
    layer.set_weights(weight)
history = model.fit_generator(
    datagen.flow(x_train, y_train, batch_size=batch_size),
    steps_per_epoch=steps_per_epoch,
    epochs=epochs,
    validation_data=(x_val, y_val),
    verbose=0,
    callbacks=[
        EarlyStopping(patience=epochs, restore_best_weights=True),
        LeNetPruneCallback(masks)
    ]
)
loss, acc = model.evaluate(x_test, y_test, verbose=0)
print("Accuracy at Early-Stop:", acc)
print(
    "Early-Stop Iteration:",
    (np.argmin(np.array(history.history["val_loss"])) + 1) * steps_per_epoch
)

Accuracy at Early-Stop: 0.9816
Early-Stop Iteration: 3600

すると、3600イテレーションで精度98.2%が達成できました。
今度は刈り込み済みネットワーク構造を、別のランダムな初期値を使って、最初から訓練しなおします。

model = get_lenet()
history = model.fit_generator(
    datagen.flow(x_train, y_train, batch_size=batch_size),
    steps_per_epoch=steps_per_epoch,
    epochs=epochs,
    validation_data=(x_val, y_val),
    verbose=0,
    callbacks=[
        EarlyStopping(patience=epochs, restore_best_weights=True),
        LeNetPruneCallback(masks)
    ]
)
loss, acc = model.evaluate(x_test, y_test, verbose=0)
print("Accuracy at Early-Stop:", acc)
print(
    "Early-Stop Iteration:",
    (np.argmin(np.array(history.history["val_loss"])) + 1) * steps_per_epoch
)

Accuracy at Early-Stop: 0.9739
Early-Stop Iteration: 5000

すると、今回は5000イテレーション（以上）で精度97.4%が達成できました。
これまでの結果を表にしてみます。

条件	イテレーション数	精度
密なネットワーク	4300	97.9%
刈り込み済みネットワークを刈り込み前と同じ初期パラメータから訓練した場合	3600	98.2%
刈り込み済みネットワークを刈り込み前と違う初期パラメータから訓練した場合	5000	97.4%

刈り込みをしたアーキテクチャで、刈り込みに使った初期パラメータから学習しなおした場合、イテレーション数も少なく済み、精度も高くなっています。これは宝くじ仮説でいうところの当たりくじの条件を満たしています。
それに比べて、初期パラメータを再度ランダムに与えなおして学習しなおした場合、イテレーション数も多くかかり、精度も低くなってしまいました。これは刈り込みで得られたネットワークアーキテクチャは、それ単独でなく初期値と組み合わせないと有用でないということを示唆しています。

論文では、別のアーキテクチャでの実験や、刈り込みの繰り返し回数を変えた実験など、さまざまな条件での実験が行われているので、興味がある方は原論文をご参照ください。

刈り込まれたネットワーク構造

刈り込み後のネットワークアーキテクチャを可視化する実験もしてみます。なお、このような可視化は論文中では行われていないと思います。
まずは、最初の全結合層のつながりを可視化します。

plt.imshow(masks[0].astype("float32"))
plt.colorbar()
plt.show()

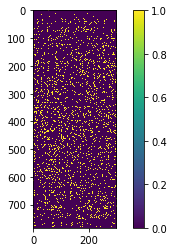
縦軸が入力画像の各ピクセルを表しており、横軸が最初の隠れ層の各ユニットを表しています。黄色く表示されている部分がつながっているところで、紫色に表示されている部分がつながっていないところです。黄色い点がおおむねばらばらに分布しているように見えます。このことから、論文の付録F.6でも指摘されていることですが、特定のユニットに接続が集中しているわけではないことが推察できます。
次に、画像の各部位から、いくつの接続が出ているかを可視化します。紫色に近いほどその位置の画素から隠れ層への接続が少なく、黄色に近いほど接続が多いです。

plt.imshow((masks[0]).sum(axis=1).reshape((28, 28)))
plt.colorbar()
plt.show()

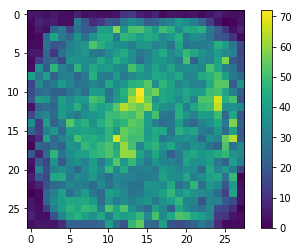
図をみると、刈り込みによって、画像の四隅の領域からはほとんど接続が失われていることがわかります。これは、手書き数字を識別するのに四隅の領域は重要でないということの現れだと思います。

まとめ

この記事では、ニューラルネットワークに関する宝くじ仮説を紹介しました。また、その実験の追試も行いました。

参考文献

• [1803.03635] The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks
• The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks | OpenReview
• Best Paper Award