Rで実践！欠損データ分析入門【2】

t2sy

2017.12.20

Topics

kNNによる代入
Random Forestによる代入
FAMDによる代入
おわりに

こんにちは。データサイエンスチームの t2sy です。
この記事は NHN テコラス DATAHOTEL：確率統計・機械学習・ビッグデータを語る Advent Calendar 2017 の20日目の記事です。
Rで実践！欠損データ分析入門【1】では BostonHousing データセットから欠損データを生成し、欠損データの可視化、MCAR検定、単一代入法と多重代入法による代入を R のコードを交えご紹介しました。引き続き、欠損データの代入に関する以下のCRANパッケージをご紹介します。

VIM
missForest
missMDA

準備として前回同様に米国ボストン市郊外における地域別の住宅価格のデータセット BostonHousing から MCAR/MAR を仮定できるような欠損データを作ります。

 > data(BostonHousing, package = "mlbench")
 > data <- BostonHousing
 > set.seed(123)
 > data.mis <- missForest::prodNA(data, noNA = 0.2)

このデータに対して kNN、missForest、FAMD による代入を行い、得られた擬似完全データについて以下を確認します。

カテゴリ変数 (chas) の分布
連続変数 (age、nox) の分布
線形回帰モデルのパラメータ推定値

kNNによる代入

k近傍法 (k-Nearest Neighbors algorithm; kNN) による代入は、特徴空間で欠測値に近い k 個のサンプルを探し集約した値で代入を行います。
特異値分解 (singular value decomposition; SVD) による代入と比較し非時系列データやノイズの多いデータに対して堅牢で性能が良いことが報告されています。(Troyanskaya, 2001)
前回、欠損データの可視化でご紹介しましたVIMパッケージを使って kNN による代入を試してみます。
VIM::kNN() ではユークリッド距離でなくGower距離を拡張した距離を用いることで、連続変数、カテゴリ変数、順序変数を扱えるようにしています。距離計算は Rcpp を用いた C++ で実装されています。(gowerD.cpp)
VIM::kNN() には近傍の数 k や集約する関数 numFun、catFun を指定します。今回 k = 5 としましたが、 k は通常奇数で交差検証 (Cross-validation) で決定するのが一般的です。
また、k 個の近傍値を集約する関数のデフォルト値は連続変数の場合に k 個の中央値、カテゴリ変数の場合に k 個の中で最も出現頻度の高いカテゴリとなります。

 > library(VIM)
 > library(dplyr)
 >
 > imp.knn <- kNN(data.mis,
 +                k = 5,
 +                imp_var = TRUE,
 +                imp_suffix = "imp")
 >
 > data.comp.knn <- imp.knn %>% select(-ends_with("_imp"))
 >
 > model.knn <- lm(medv ~ ., data = data.comp.knn)
 > summary(model.knn)
 Call:
 lm(formula = medv ~ ., data = data.comp.knn)
 Residuals:
 Min       1Q   Median       3Q      Max
 -11.3193  -2.8929  -0.7699   1.9532  27.3785
 Coefficients:
 Estimate Std. Error t value Pr(>|t|)
 (Intercept)  42.342213   5.692423   7.438 4.57e-13 ***
 crim         -0.052548   0.041541  -1.265 0.206478
 zn            0.011360   0.014579   0.779 0.436241
 indus        -0.063208   0.063805  -0.991 0.322347
 chas1         2.861072   1.079247   2.651 0.008284 **
 nox         -18.833362   4.188530  -4.496 8.63e-06 ***
 rm            3.324085   0.463759   7.168 2.81e-12 ***
 age           0.008536   0.014918   0.572 0.567448
 dis          -1.239408   0.206345  -6.006 3.69e-09 ***
 rad           0.230685   0.069221   3.333 0.000925 ***
 tax          -0.007908   0.003966  -1.994 0.046709 *
 ptratio      -1.096212   0.138296  -7.927 1.52e-14 ***
 b             0.007566   0.002957   2.559 0.010803 *
 lstat        -0.560159   0.055885 -10.023  < 2e-16 ***
 ---
 Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 Residual standard error: 5.01 on 492 degrees of freedom
 Multiple R-squared:  0.6994,	Adjusted R-squared:  0.6914
 F-statistic: 88.04 on 13 and 492 DF,  p-value: < 2.2e-16

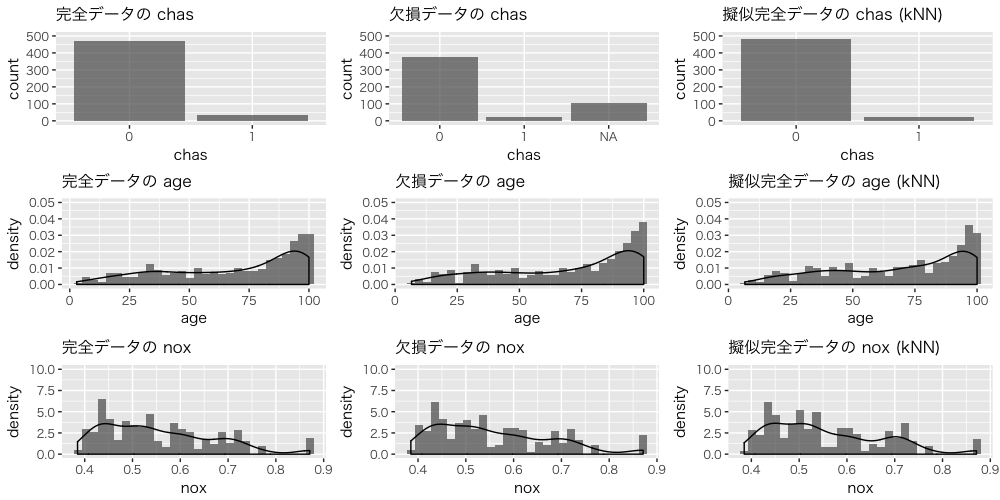
完全データ、欠損データ、擬似完全データの chas、age、nox の分布を確認します。

Random Forestによる代入

missForest は Random Forest を用いたノンパラメトリックな代入法です。 Random Forest は決定木のアンサンブル法の代表的手法で、バギングに加えてランダムな特徴選択を取り入れています。
Random Forest は非線形性を学習でき、混合型データ (mixed-type data) の扱いが容易、OOB (out-of-bag) Error を計算できるという特徴がありますが missForest でもこれらの利点を生かしています。
実際に、missForestパッケージは内部でrandomForestパッケージを使用しています。
missForest のアルゴリズムを論文から引用します。

n x p の行列 X について対象の変数を Xs として y_s_mis は Xs の欠測値、 x_s_mis は Xs 以外の対象行の観測値、 y_s_obs は Xs の観測値、 x_s_obs は Xs 以外の対象行を除く観測値とします。以下のようなイメージです。

ざっくりとしたアルゴリズムの流れは以下です。

欠測値を初期値で代入した n x p の行列 X を作成
停止基準 γ に達するまで 3 を繰り返す
X に含まれる全ての変数について 4、5 を繰り返す
対象の変数 Xs について y_s_obs を目的変数、x_s_obs を説明変数として Random Forest で学習
4 のモデルを使って x_s_mis から y_s_mis を予測し X を更新

停止基準 γ はイテレーションが事前に設定した最大値に達するか以下で計算される代入済みデータ行列の差が前回より低下しなくなった場合, つまり予測が安定した状態となります。
連続変数の集合 N に対する差は以下で計算されます。
$\triangle_{N} = \frac{\sum_{j \in N}(X^{imp}_{new} - X^{imp}_{old})^2}{\sum_{j \in N}(X^{imp}_{new})^2}$
また、カテゴリ変数の集合 F に対する差は以下で計算されます。 #NA はカテゴリ変数中の欠測値の数です。
$\triangle_{F} = \frac{\sum_{j \in F}\sum^{n}_{i=1}I_{X^{imp}_{new} \neq X^{imp}_{old}}}{ \#NA }$
R で missForest を試してみます。以下の例ではdoParallelパッケージにより処理を並列化しています。

 > library(missForest)
 > library(doParallel)
 > cores <- detectCores(logical = FALSE)
 > registerDoParallel(cores = cores)
 > imp.mf <- missForest(data.mis,
 +                      maxiter = 10,
 +                      ntree = 100,
 +                      mtry = floor(sqrt(ncol(data.mis))),
 +                      parallelize = "variables",
 +                      verbose = TRUE)
 parallelizing over the variables of the input data matrix 'xmis'
 missForest iteration 1 in progress...done!
 estimated error(s): 0.1658196 0.07518797
 difference(s): 0.01739636 0.003952569
 time: 2.516 seconds
 missForest iteration 2 in progress...done!
 estimated error(s): 0.152469 0.08270677
 difference(s): 0.0003366006 0.001976285
 time: 1.649 seconds
 missForest iteration 3 in progress...done!
 estimated error(s): 0.1563453 0.0726817
 difference(s): 0.0001837863 0.001976285
 time: 1.612 seconds
 missForest iteration 4 in progress...done!
 estimated error(s): 0.1554296 0.07769424
 difference(s): 0.0001856931 0.001976285
 time: 1.559 seconds
 > imp.mf$OOBerror
 NRMSE       PFC
 0.1563453 0.0726817
 > data.comp.mf <- imp.mf$ximp
 > model.mf <- lm(medv ~ ., data = data.comp.mf)
 > summary(model.mf)
 Call:
 lm(formula = medv ~ ., data = data.comp.mf)
 Residuals:
 Min       1Q   Median       3Q      Max
 -11.8579  -2.6266  -0.5817   1.6656  27.3486
 Coefficients:
 Estimate Std. Error t value Pr(>|t|)
 (Intercept)  39.771809   5.743747   6.924 1.37e-11 ***
 crim         -0.076848   0.038727  -1.984 0.047772 *
 zn            0.053070   0.014767   3.594 0.000359 ***
 indus         0.032570   0.062222   0.523 0.600899
 chas1         3.662500   0.961835   3.808 0.000158 ***
 nox         -20.866061   4.142871  -5.037 6.66e-07 ***
 rm            3.801596   0.451928   8.412 4.40e-16 ***
 age           0.011089   0.015045   0.737 0.461434
 dis          -1.500017   0.217307  -6.903 1.58e-11 ***
 rad           0.296862   0.068638   4.325 1.85e-05 ***
 tax          -0.012444   0.003934  -3.163 0.001656 **
 ptratio      -1.024917   0.136477  -7.510 2.81e-13 ***
 b             0.006823   0.002885   2.365 0.018438 *
 lstat        -0.531227   0.054287  -9.786  < 2e-16 ***
 ---
 Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 Residual standard error: 4.611 on 492 degrees of freedom
 Multiple R-squared:  0.7481,	Adjusted R-squared:  0.7414
 F-statistic: 112.4 on 13 and 492 DF,  p-value: < 2.2e-16

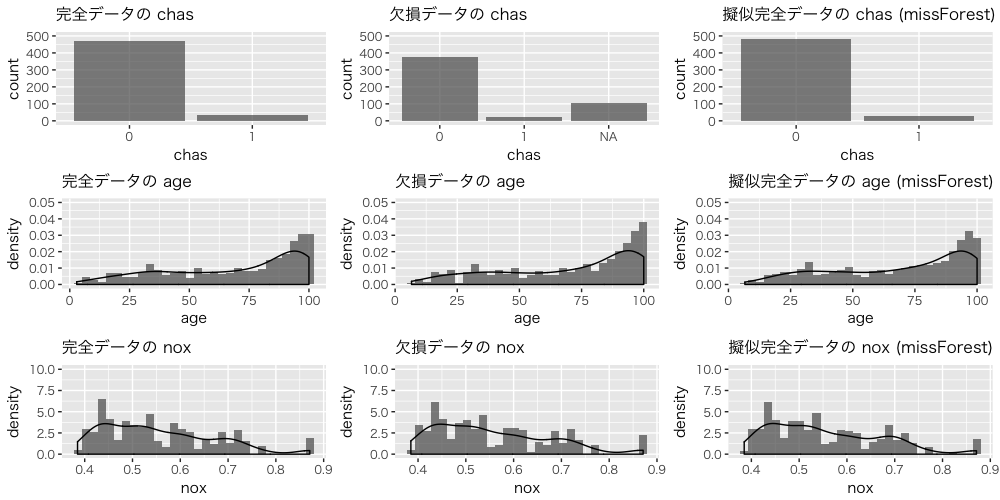
完全データ、欠損データ、擬似完全データの chas、age、nox の分布を確認します。

FAMDによる代入

missMDAパッケージは、主成分分析 (Principal Component Analysis; PCA)、多重対応分析 (Multiple Correspondence Analysis; MCA)、多因子分析 (Multiple Factor Analysis; MFA) といった多変量解析に基づく代入を行います。
FAMD (Factor Analysis for Mixed Data) は混合データを扱える MFA の特別な場合で、FAMD による代入 (Audigier et al., 2013) は連続変数とカテゴリ変数間の類似度を考慮し欠測値に代入することができます。特に稀なカテゴリが欠測している場合や、変数間に線形的な関係がある場合に良い予測が得られるようです。論文では missForest との比較にも言及しているので興味がある方は参考文献をご参照ください。
今回のデータは混合データのため FAMD を試してみます。
まず、estim_ncpFAMD() で欠測値を予測する時に使う主成分の次元数を交差検証により推定します。
次に、imputeFAMD() の ncp に推定された次元数、method に Regularized を指定し、正規化反復FAMD (Regularized Iterative FAMD) を実行します。
反復はパラメータ推定と予測値の欠測値への代入を収束するまで繰り返し実行することを意味します。また、正規化を行うことでノイズが多かったり欠測値が多い場合に予測性能が低下する問題を改善しています。

 > library(missMDA)
 > dims <- estim_ncpFAMD(data.mis,
 +                       method = "Regularized",
 +                       method.cv = "kfold",
 +                       nbsim = 100,
 +                       pNA = 0.20)
 |===============================================================| 100%
 > imp.famd <- imputeFAMD(data.mis,
 +                        ncp = dims$ncp,
 +                        method = "Regularized")
 > data.comp.famd <- imp.famd$completeObs
 >
 > model.famd <- lm(medv ~ ., data = data.comp.famd)
 > summary(model.famd)
 Call:
 lm(formula = medv ~ ., data = data.comp.famd)
 Residuals:
 Min       1Q   Median       3Q      Max
 -11.7413  -2.4143  -0.6447   1.7322  26.1426
 Coefficients:
 Estimate Std. Error t value Pr(>|t|)
 (Intercept)  41.984471   5.637290   7.448 4.29e-13 ***
 crim         -0.073707   0.040018  -1.842  0.06610 .
 zn            0.024324   0.015016   1.620  0.10590
 indus        -0.074326   0.061136  -1.216  0.22467
 chas1         3.187217   0.995469   3.202  0.00145 **
 nox         -20.643686   4.180986  -4.938 1.09e-06 ***
 rm            3.412203   0.452140   7.547 2.18e-13 ***
 age           0.014872   0.014968   0.994  0.32091
 dis          -1.269515   0.209020  -6.074 2.50e-09 ***
 rad           0.240479   0.057605   4.175 3.53e-05 ***
 tax          -0.006017   0.003256  -1.848  0.06519 .
 ptratio      -1.111493   0.131693  -8.440 3.57e-16 ***
 b             0.007332   0.002963   2.474  0.01369 *
 lstat        -0.549031   0.053637 -10.236  < 2e-16 ***
 ---
 Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 Residual standard error: 4.576 on 492 degrees of freedom
 Multiple R-squared:  0.7492,	Adjusted R-squared:  0.7426
 F-statistic:   113 on 13 and 492 DF,  p-value: < 2.2e-16

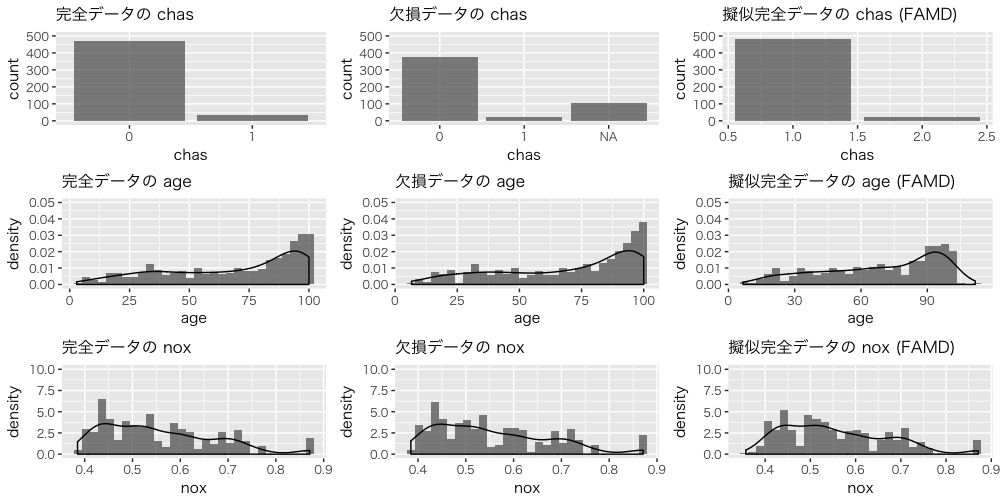
完全データ、欠損データ、擬似完全データの chas、age、nox の分布を確認します。

最後に、完全データと3つの擬似完全データから作成した線形回帰モデルのパラメータ推定値を確認します。以下のプロットにはcoefplotパッケージを使用しています。

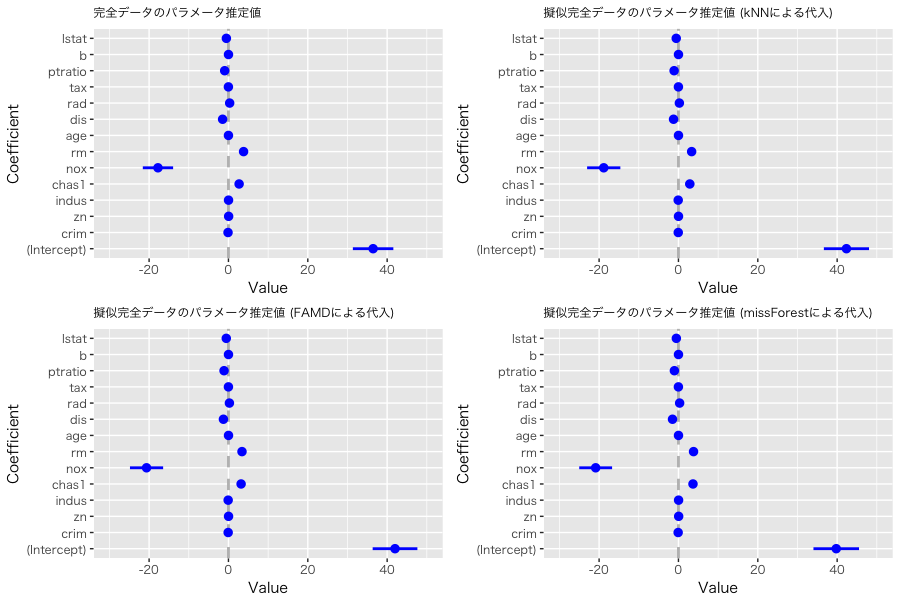
今回のデータに対しては kNN、missForest、FAMD のいずれもそこそこの精度で推定できていると思います。
(ちゃんとした性能比較を期待されていた方には申し訳ありませんが、今回は主題がCRANパッケージの紹介ということでご了承下さい)

おわりに

今回は kNN、missForest、FAMD による代入をご紹介しました。 Missing Data Imputation etc: Literature and R packages に紹介しきれなかったCRANパッケージ含め代入法別にパッケージがまとめられているので興味がある方はご覧下さい。
実世界のデータは欠測値を含んでいることが多くありますが、欠損データをどのように扱うかは後続の分析にも大きな影響を与えます。
そのため、欠測メカニズムを含めたデータの性質に応じて適切な処理を選択することが重要だと思います。一方で、複数の代入法を試し結果を比較することで気づく点もあるかもしれません。
前回と今回の記事が少しでも分析のお役に立てれば幸いです。