可分な畳み込みカーネルと計算量の話
こんにちは。データサイエンスチームのtmtkです。
この記事では、可分なカーネルによる畳み込みと計算量の説明をします。
畳み込みとは
はじめに畳み込みを復習します。
機械学習において、畳み込みとは以下のような処理です。いま、入力が2次元の場合を考えることにします。畳み込みカーネルをとするとき、入力
に対するカーネル
による畳み込み
は、
に対して
で定義されます。
畳み込みは、古典的な画像処理や最近流行りのディープラーニングでも用いられています。画像認識の本やディープラーニングの本に詳しいことが書かれています。
Pythonで書く畳み込み処理
Pythonで実際に畳み込み処理を書いてみます。コンピュータで処理するため、入力とカーネル
は0-originなindexを持つとします。つまり、行列として表示すると
となります。
いま、入力のサイズを
N = 10 n = 3 image = [[1] * N for _ in range(N)] kernel = [[1] * n for _ in range(n)]
すると、畳み込みを計算するPythonの関数は以下のように書くことができます。
def convolution(image, kernel):
N1 = len(image)
N2 = len(image[0])
n1 = len(kernel)
n2 = len(kernel[0])
res = [[0] * N2 for _ in range(N1)]
for i in range(N1):
for j in range(N2):
for k in range(min(n1, N1 - i)):
for l in range(min(n2, N2 - j)):
res[i][j] += image[i+k][j+l] * kernel[k][l]
return res
実際に計算してみると、
convolution(image, kernel)
以下のような畳み込みの計算結果を得ます。
[[9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [6, 6, 6, 6, 6, 6, 6, 6, 4, 2], [3, 3, 3, 3, 3, 3, 3, 3, 2, 1]]
可分な畳み込みカーネル
ところで、いま与えた畳み込みカーネルは可分なカーネルの例になっています。2次元のカーネル
が可分であるとは、二つのベクトル
によって
と書けることをいいます。先ほどのカーネル
は、
(ただし
可分なカーネルの例としては、他にも平均値をとるカーネル
や、ガウス関数から作られるカーネル
などがあります。
可分なカーネル
証明は簡単なので省略します。
それでは、この性質を使って先ほどの畳み込みを計算してみましょう。関数
convolution_separableは可分なカーネル
kernel1 = [1]*n
kernel2 = [1]*n
def convolution_separable(image, kernel1, kernel2):
N1 = len(image)
N2 = len(image[0])
n1 = len(kernel1)
n2 = len(kernel2)
res = [[0] * N2 for _ in range(N1)]
tmp = [[0] * N2 for _ in range(N1)]
for i in range(N1):
for j in range(N2):
for k in range(min(n1, N1 - i)):
tmp[i][j] += image[i+k][j] * kernel1[k]
for i in range(N1):
for j in range(N2):
for l in range(min(n2, N2 - j)):
res[i][j] += tmp[i][j+l] * kernel2[l]
return res
convolution_separable(image, kernel1, kernel2)
[[9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [9, 9, 9, 9, 9, 9, 9, 9, 6, 3], [6, 6, 6, 6, 6, 6, 6, 6, 4, 2], [3, 3, 3, 3, 3, 3, 3, 3, 2, 1]]
先ほどの計算方法と同じ結果を得ることができます。
それぞれの方法の計算量
それぞれの計算方法について、処理時間を見積もってみましょう。
最初の方法では、関数convolutionに四重ループ
for i in range(N1):
for j in range(N2):
for k in range(min(n1, N1 - i)):
for l in range(min(n2, N2 - j)):
があり、ループが約回実行されます。いま、
とおけば、ループの回数は
回以下です。そのため、この関数の処理時間は
にほぼ比例すると考えることができます。このような状況をさして、この関数は時間計算量が
であるといいます。
それに対して、可分なカーネルに対する畳み込みでは、関数convolution_separableに以下の2つの三重ループがあります。
for i in range(N1):
for j in range(N2):
for k in range(min(n1, N1 - i)):
for i in range(N1):
for j in range(N2):
for l in range(min(n2, N2 - j)):
そのため、このconvolution_separableの処理時間はにほぼ比例すると考えることができ、時間計算量は
です(
と書くときは、定数倍を無視します)。
したがって、計算量がそれぞれで、前者より後者のほうが小さいため、
が大きいとき関数
convolutionよりconvolution_separableのほうが計算時間が短くなることが予想できます。
実際の計算時間
それでは、時間計算量が実際の計算時間に及ぼす影響を観察するため、どれくらいの処理時間がかかるのか計測してみます。
計算環境はCore i7が載っている普通のパソコン上の仮想マシンです。として、
を変動させながら、畳み込み処理にかかった時間をIPythonのマジックコマンド
%timeで計測します。
N = 1000 image = [[1] * N for _ in range(N)]
たとえば、のとき、次のようなコードで処理時間を算出します。
n = 10 %time convolution(image, [[1] * n for _ in range(n)]) %time convolution_separable(image, [1]*n, [1]*n)
結果は以下のようになります。関数convolutionの処理時間がに比例していることと、関数
convolution_separableの処理時間がに比例していることが観察できます。
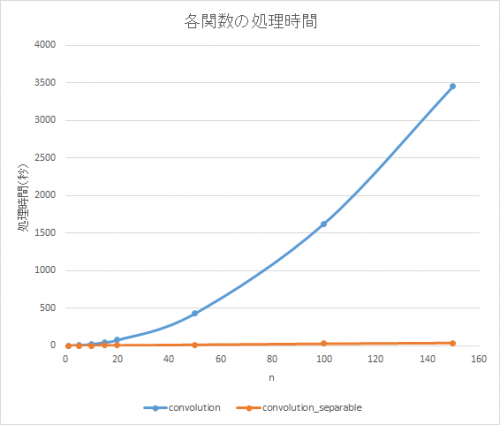
ここから推定すると、
convolutionの処理時間はおよそ10時間程度かかってしまうのにたいして、convolution_separableの処理時間はたったの2分程度になります。時間計算量がこのように、大きいデータを処理するとき、時間計算量を考慮することは重要です。
まとめ
この記事では、可分なカーネルでの畳み込みの効率的な計算方法と、それによる時間計算量の差について説明しました。可分なカーネルでの畳み込みは、通常の畳み込みよりも高速に計算することができます。時間計算量の差は大きなデータになると実際の処理時間の差に如実に現れてくるので、時間計算量を考慮したアルゴリズムを設計することが大切です。
参考文献
- 原田達也『画像認識』
- Ian Goodfellow他『深層学習』
- Separable convolution » Steve on Image Processing – MATLAB & Simulink
- ランダウの記号 – Wikipedia
- 8.2. コンボリューション行列…
- 畳み込みを画像処理に適用した例が載っています。
テックブログ新着情報のほか、AWSやGoogle Cloudに関するお役立ち情報を配信中!
Follow @twitterデータ分析と機械学習とソフトウェア開発をしています。 アルゴリズムとデータ構造が好きです。
Recommends
こちらもおすすめ
-

R からシームレスに Python を呼べる reticulate が便利だった
2018.4.13
-

社内エンジニア読書会の進め方 ーAI・機械学習チーム編ー
2019.4.4
-

口コミデータを活用したレコメンドシステムの可能性
2017.12.7
Special Topics
注目記事はこちら

データ分析入門
これから始めるBigQuery基礎知識
2024.02.28

AWSの料金が 10 %割引になる!
『AWSの請求代行リセールサービス』
2024.07.16



