Amazon Personalize を活用した記事推薦システムを自社ブログに導入した話 (2)

t2sy

2020.2.20

Topics

ベイズ推論によるA/Bテスト
おわりに

こんにちは。データサイエンスチームの t2sy です。

2019年10月に紹介しました Amazon Personalizeを活用した記事推薦システムを自社ブログに導入した話 (1) では、テックブログに推薦システムを導入した背景と構成、設計時に意識した点について紹介しました。今回は、推薦システム導入後に行ったベイズ推論によるA/Bテストについて紹介します。

関連記事: Amazon Personalizeを活用した記事推薦システムを自社ブログに導入した話(1)

ベイズ推論によるA/Bテスト

推薦システム全体の構成は以下となります。

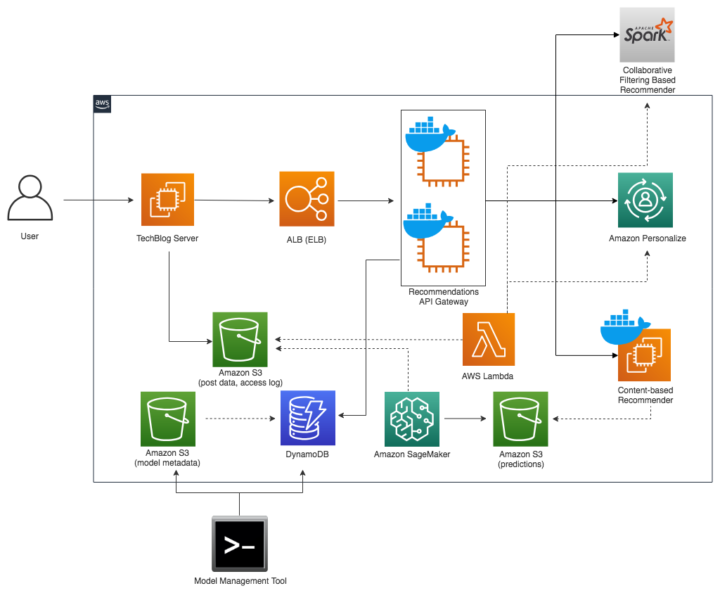
図中の Recommendations API Gateway は記事ページへのリクエストに対して、背後の複数のモデルからランダムにモデルを選択し推薦を取得します。
A/Bテストの期間や配信回数などのモデル管理の情報は Amazon DynamoDB に保存しています。期間を過ぎたり配信回数を超えた場合、Recommendations API Gateway は対象のモデルからの API による推薦の取得を停止します。また、同時に Amazon DynamoDB Triggers の機能を用いて Slack へ通知が行われます。

ベイズ推論

A/Bテストでは Neyman-Pearson 流 [1] の統計的仮説検定が広く使われています。今回は、ベイズ推論の視点からA/Bテストの分析を行ってみます。

最初に、今回のA/Bテストのデータ生成過程を考えてみます。ユーザはテックブログ記事の閲覧時に表示される推薦に対して、2通りの反応 $x_{i} \in \{0,1\}$ を示します。推薦をクリックした場合は $x_{i} = 1$ 、クリックしなかった場合は $x_{i} = 0$ です。これは、パラメータ $\theta$ のベルヌーイ分布からの実現値であると考えられます。

$p(x_{i}) = \theta^{x_{i}}(1-\theta)^{1-x_{i}}$

また、推薦を独立に n 回繰り返し、その内 k 回クリックされたという現象は二項分布で表すことができます。

$p(k) = \left( \begin{array}{cc} n\\ k\\ \end{array} \right) \theta^k(1-\theta)^{n-k} = \frac{n!}{(n-k)!k!} \theta^k(1-\theta)^{n-k}$

$n=1, k \in \{0,1\}$ の二項分布はベルヌーイ分布となります。

ベイズの定理は観測データを $x$ , パラメータを $\theta$ として以下です。

$p(\theta_{i}|x) = \frac{p(\theta_{i})p(x|\theta_{i})}{\sum_{i=1} p(x|\theta_{i})p(\theta_{i})}$

上の式で右辺の分母を定数として扱うと、事後分布 $p(\theta|x)$ は事前分布 $p(\theta)$ と尤度 $p(x|\theta)$ の積に比例する関係であることがわかります。

$p(\theta|x) \propto p(\theta)p(x|\theta)$

ベイズの定理を用いて事後分布を計算するために、事前分布を設定する必要があります。事前分布に共役事前分布を用いると、複雑な計算を回避できます。個々の観測がベルヌーイ分布に従う場合では、共役事前分布としてベータ分布を用いることができます。ベータ分布は以下で表されます。

$p(\theta | \alpha, \beta) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\theta^{\alpha-1}(1-\theta)^{\beta-1}$

上の式の先頭の係数は規格化のための定数として扱うこととします。

最初に、観測データはベルヌーイ分布に従うと仮定しました。ベルヌーイ分布の尤度は以下です。

$L(\theta|x) = \prod_{i=1}^n \theta^{x_{i}}(1-\theta)^{1-x_{i}}$

事前分布 (ベータ分布) とベルヌーイ分布の尤度の積から事後分布を導きます。n 回の試行でクリックされた回数を $k = \sum_{i=1}^n x_{i}$ と置いています。

$p(\theta | \alpha, \beta, x) \\\propto p(\theta | \alpha, \beta) \prod_{i=1}^n \theta^{x_{i}}(1-\theta)^{1-x_{i}} \\\propto \theta^{\alpha-1}(1-\theta)^{\beta-1} \theta^{\sum_{i=1}^n x_{i}}(1-\theta)^{n-\sum_{i=1}^n x_{i}} \\= \theta^{\alpha-1}(1-\theta)^{\beta-1} \theta^k(1-\theta)^{n-k} \\= \theta^{\alpha-1+k}(1-\theta)^{\beta-1+n-k}$

規格化のための定数を伴った場合、 $Beta(\alpha+k, \beta+n-k)$ となり、事後分布もベータ分布であることが確認できます。
また、ベータ分布のパラメータ $\alpha, \beta$ が共に 1 の場合は一様分布と一致します。従って、事前分布を一様分布とすると、事後分布は $Beta(1+k, 1+n-k)$ となります。

簡単な具体例で考えてみます。事前分布を一様分布 $Beta(1, 1)$ とし、ベルヌーイ分布に従う観測データ $x = \{0,0,1,0,0,0,1,0,0,0\}$ が得られたとすると、事後分布は $Beta(3, 9)$ です。事後分布の期待値と分散は以下となります。

$E[x] = \frac{\alpha}{\alpha+\beta} = 0.25 \\ V[x] = \frac{\alpha\beta}{(\alpha+\beta)^2 (\alpha+\beta+1)} = 0.0144$

得られた事後分布を次の事前分布と置くことで、逐次的に分布を更新することができます。

複雑な階層モデルなどパラメータ空間が高次元となる場合、積分を解析的に処理できないケースが出てきます。その解決策として MCMC (Markov Chain Monte Carlo) により事後分布からサンプリングを行い、その分布を調べることでパラメータ推定を行う方法がよく用いられます。一方で、今回のように解析的に事後分布を求めることが容易な場合は MCMC に比べ計算量が少なくて済みます。

今回は、実験も兼ねて MCMC を用いたベイズ推論を行ってみます。

ベイズ推論によるA/Bテスト

以下の2つの推薦手法のA/Bテストを行います。

Previous Method: 推薦システム導入前の方法で、同一タグ・同一カテゴリ・同一投稿者の記事からランダムに選択
Content-based Recommender (M-USE): 各記事の要約に対して「Multilingual Universal Sentence Encoder for Semantic Retrieval」[3] の学習済みモデル [5] で埋め込みを計算、記事間の類似度を内積を取り計算

今回のA/Bテストでは、上記の2つの推薦手法をリクエスト単位でランダムに割り当てます。
2週間のA/Bテスト実施後、アクセスログを集計し以下の列から成る表データを抽出します。

列名	意味
access_log_dt	記事ページのリクエスト時に Web サーバのアクセスログに記録された日時
model_id	モデルを一意に識別するための文字列
click	推薦がクリックされたか否かの二値 (i.e. $x_{i} \in \{0,1\}$ )
nonce_dt	レスポンスに付与するタイムスタンプの日時表現

上記の nonce_dt 列は、他の列と組み合わせて短時間に連続するリクエストを同一のリクエストと見なすための手がかりや、A/Bテスト開始以前の推薦からのクリックを取り除くために使用しています。

データの準備ができたので、MCMC によるベイズ推論を実行してみます。今回は Python を用います。
Python でベイズ推論をサポートするライブラリは PyMC3、PyStan、Edward、TensorFlow Probability など複数の選択肢があります。
以前、確率的プログラミング言語 Stan を使用したことがあることから Stan へのインターフェイスを提供する PyStan を選択しました。Stan は MCMC のアルゴリズムに HMC (Hamiltonian Monte Carlo) の一実装である NUTS (No-U-Turn-Sampler) を用いています。

Previous Method をモデルA、Content-based Recommender (M-USE) をモデルBと置き、パラメータ $\theta_{A}$ , $\theta_{B}$ と、モデル間の差 $\delta_{\theta} = \theta_{A} - \theta_{B}$ を調べてみます。

環境は Python 3.7.4、PyStan 2.19.0.0 です。

以下のシンプルな Stan のコードを書きます。

import pystan

stan_code = """
data {
    int<lower=0> N;
    int<lower=0> M;
    int<lower=0,upper=1> x_A[N]; // observations of model A
    int<lower=0,upper=1> x_B[M]; // observations of model B
}

parameters {
    real<lower=0,upper=1> theta_A;
    real<lower=0,upper=1> theta_B;
}

transformed parameters {
    real delta;
    delta = theta_A - theta_B;
}

model {
    x_A ~ bernoulli(theta_A);
    x_B ~ bernoulli(theta_B);
}
"""

pystan.StanModel() の model_code 引数に Stan のコードを指定し、インスタンス化します。

ab_data = {'N': len(observations_A),
           'M': len(observations_B),
           'x_A': observations_A,
           'x_B': observations_B}

sample_size = 5000
warmup_rate = 0.2

sm = pystan.StanModel(model_code=stan_code)
fit = sm.sampling(data=ab_data,
                  seed=42,
                  warmup=int(sample_size*warmup_rate),
                  iter=sample_size,
                  chains=4)

インスタンスに対して MCMC を実行する sampling メソッドを呼び出す際の data 引数に観測データ (click 列) を指定し、データをモデルに取り込みます。
MCMC が完了すると StanFit4Model オブジェクトが返されます。これを print() に渡すと、一連のサンプルの要約が得られます。諸事情のため一部の数値は伏せております。

Inference for Stan model: anon_model_1bd7c2e3c1caffbf7528e280136cb510.
4 chains, each with iter=5000; warmup=1000; thin=1; 
post-warmup draws per chain=4000, total post-warmup draws=16000.

          mean se_mean     sd   2.5%    25%    50%    75%  97.5%  n_eff   Rhat
theta_A   ****  ****** ******   ****   ****   ****   ****   ****  *****    1.0
theta_B   ****  ****** ******   ****   ****   ****   ****   ****  *****    1.0
delta    -0.02  5.6e-5 6.7e-3  -0.03  -0.02  -0.02  -0.01-2.5e-3  14251    1.0
lp__    -323.8    0.01    1.0 -326.5 -324.2 -323.5 -323.1 -322.8   7190    1.0

Samples were drawn using NUTS at Tue Feb  4 11:54:25 2020.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

収束の判断基準のひとつである Rhat はいずれも 1.0 です。

$\theta_{A}$ , $\theta_{B}$ の事後分布は以下です。

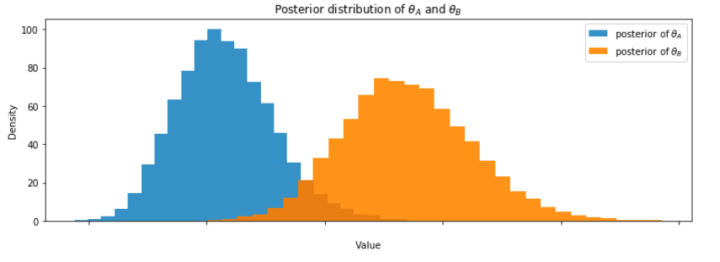
また、興味のある $\theta_{A}$ と $\theta_{B}$ の差を示す $\delta_{\theta}$ の事後分布は以下です。

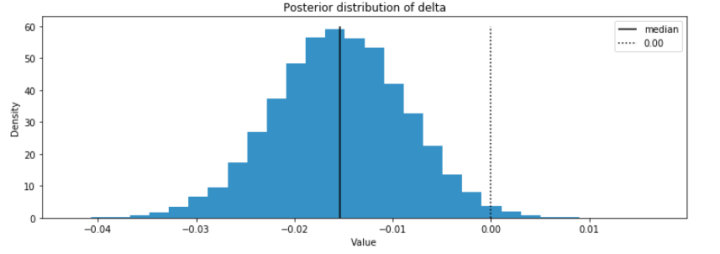
モデルBがモデルAより良い確率は $\delta_{\theta}$ の事後分布の 0 より左側の面積の割合で求めることができます。
ベイズ推論の枠組みにおいて Content-based Recommender (M-USE) のモデルが Previous Method より CTR が高い確率は 99.0% と推測されました。解析的に計算した場合も、ほぼ同じ値が得られます。そのため、前者のモデルへ切り替えることを決めました。
一方で、 $\delta_{\theta}$ のベイズ信頼区間の95%信頼区間は -0.03 から -0.0025 と 0 に非常に接近しており、強い確信を得るには至らない結果と言えそうです。この要因として、今回のA/Bテストでは推薦の表示位置は記事ページの下部であることから、推薦まで辿り着く可能性は高くはなく、モデル間での大きな差に繋がらなかったことや、Previous Method における同一タグ・同一カテゴリなどメターデータの活用がそれなりに機能していた可能性などが考えられます。

Amazon Personalize

上記のA/Bテストと別の期間で、Previous Method と Amazon Personalize (HRNN-Metadata) の A/B テストを行いました。

Previous Method: 推薦システム導入前の方法で、同一タグ・同一カテゴリ・同一投稿者の記事からランダムに選択
Amazon Personalize (HRNN-Metadata): 個人にカスタマイズした推薦を作成できる完全マネージド型の AWS のサービスである Amazon Personalize の HRNN-Metadata レシピを用いて、記事のカテゴリとタグを追加の特徴として使用したモデル

Amazon Personalize の HRNN (Hierarchical Recurrent Neural Network) レシピは、セッション中のユーザーの振る舞いの変化をモデル化し推薦を提供します。テックブログへのアクセスは多くが Web 検索エンジンや SNS からの流入で、最新記事の一覧やカテゴリ、あるいは閲覧中の記事内のオススメ記事を経由することで各セッションの閲覧履歴が作られます。しかし、サイト内検索型の EC サイトと比較した場合、セッション中の閲覧履歴の長さは短い傾向があると考えました。そのため、今回は HRNN をベースとしつつ記事のカテゴリとタグを追加の特徴として使用する HRNN-Metadata レシピを用いることにしました。

分析方法は Previous Method と Content-based Recommender (M-USE) のA/Bテストと同様です。

$\delta_{\theta}$ の事後分布は以下となりました。

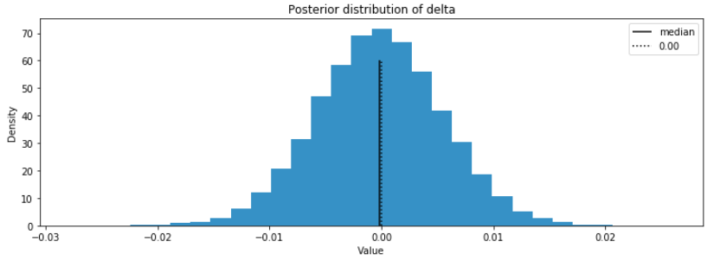
今回の結果では、Previous Method と Amazon Personalize (HRNN-Metadata) でモデル間の差はほとんどないことが窺えます。Amazon Personalize の HRNN-Metadata レシピを使用したモデルの改善点として、閲覧履歴の学習データの追加、特徴の追加、自動の HPO (Hyper Parameter Optimization) でカバーされないハイパーパラメータの最適化などが考えられます。

Amazon Personalize は HRNN や HRNN-Metadata 以外にも協調フィルタリングに基づくレシピなども提供しています。また、データが大規模になるに連れて完全マネージド型サービスとしての利点を生かすことができます。

おわりに

この記事では、推薦システム導入後に行ったベイズ推論によるA/Bテストについて紹介しました。A/Bテストで得られたデータをベイズ推論で分析し、従来法から Multilingual Universal Sentence Encoder を用いたモデルへの切り替えを決めました。今後も、システム運用監視と同様に機械学習モデルも継続的な監視・改善を行なっていきたいと思います。
MCMC を用いたベイズ推論については参考文献 [5]、[6]、Stan を用いたベイズ統計モデリングについては参考文献 [6]、[7] をご覧下さい。