お久しぶりです。橘です。
1ヶ月経ってしまいました。月2回くらいの更新頻度の予定だったのですが。。。
前回、想像ゲームというゲームで機械学習の雰囲気を
味わっていただきました。今回は想像ゲームをもう少し、実際の機械学習に近づけてみたいと思います。
一度に曲線フィッテングを書いてしまおうと思ったのですが、前編後編に分けました。
前編では、実際に曲線フィッティングを試します。
後編では、具体的にどのような仕組みで曲線フィッティングが行われているかをご紹介します。

曲線フィッティングって

曲線フィッティングとは、データに合うように曲線を引き、新たなデータを予測するものです。
言葉で説明するたびに本質から離れていってしまう（気がする）ため、数式と図を交えながらご紹介したいと思います。

曲線を数式（多項式）で表してみる

曲線は、多項式と呼ばれる曲線で表すことができます。n次元の曲線fは、次のとおりです。
（n次元というのは、多ければ多いほど曲線が曲がっていると考えて下さい。）

シグマで表現すれば、

です。なぜそうなるのか、というところは説明すると曲線フィッティングから離れていってしまうため、曲線と多項式の関係を見てみたいと思います。

sin、cosと多項式

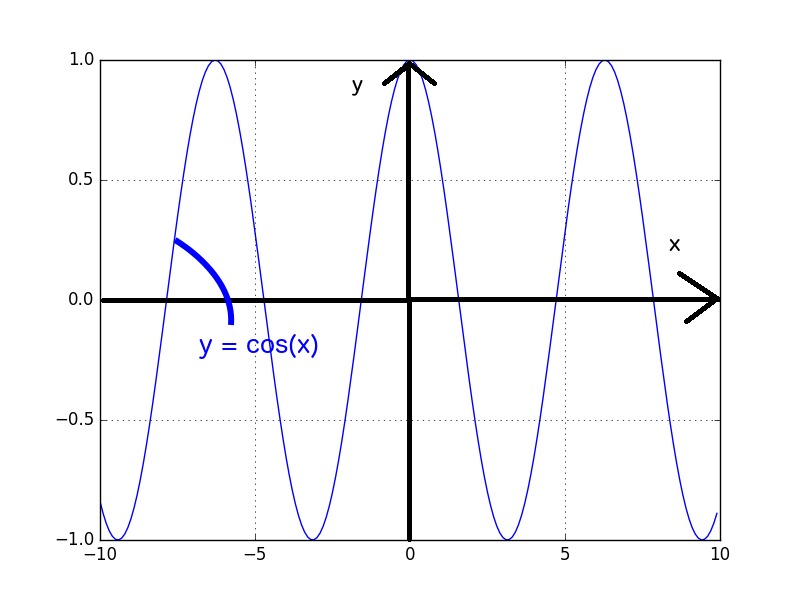
高校で習った、sin、cosは覚えているでしょうか？sin、cosの厳密な定義はさておき、sinとcosは次のようなグラフを描きます。

誰がなんと言おうとも曲線です。そして、sinとcosは、次のような多項式（厳密には級数ですが）で表すことができます。
（詳しくは、テイラー展開をお調べください。）


見比べてみると、なんとなくcos（sinでもいいのですが）の式と多項式が似ていることがわかるかと思います。

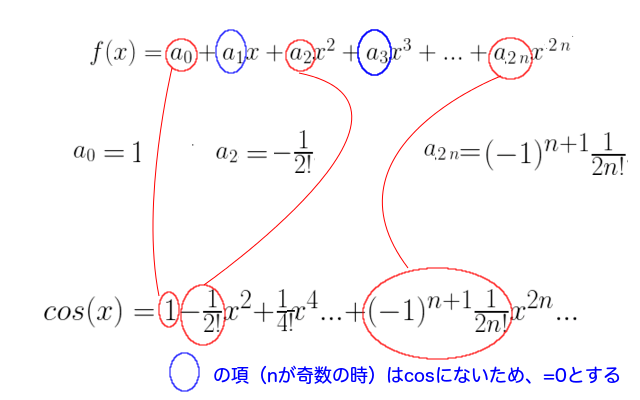
どうやら、a_0, a_1, …, a_n の値を調節してやることで、曲線を表す多項式が描けそうな気は、、、そんなにしないですよね。
ここまで説明しておいて最終的には強引ですが、曲線は多項式で表せる、のです。今後多項式が出てきても、「曲線を描こうとしているんだな」と思ってもらえれば大丈夫です。式の複雑さに惑わされないで下さい。

曲線フィッティングをしてみる

色々と都合がいいため、Pythonでコードを書いています。
Pythonのインストール方法などは、手前味噌ですがこちらのブログをご覧ください。「やりたいけどどうしてもわからない」場合は、Facebookのメッセージなどでお問い合わせください。喜んで答えます。
また、githubにも今回使ったコードをアップロードしますので、ご自由にお使い下さい。
※ソースコードの改変、再配布は認めますが、一切の責任は持たないことをご了承して頂いた上でご利用下さい。
umentu/techblog_polynomial_fitting
pipを利用している場合は、

pip install -r requirements.txt

を実行することで、必要なライブラリをインストールすることができます。
今回、アクセス数をカウントしたデータ「access_data.csv」を使って曲線フィッティングを行ってみます。a
access_data.csvの中身は次のようになっています。

1,1688
2,1736
3,1474
4,1770
5,1348
6,1570
7,1861
8,1458
9,2282
10,1553
11,2323
12,1202
13,1768
14,2184
15,1329
16,1781
17,1242
・・・・・・・・・

まず、access_data.csvを単純にプロットします。プロットするには、curve_fitting.pyを実行します。

# -*- coding; utf-8 -*-
import os
import matplotlib.pyplot as plt
import scipy as sp
def plot_data(csv_file):
    """
    データをプロットする関数
    csv_file:
    以下のような形式のCSVファイル
    ---------------
    1,1
    2,10
    3,100
    ・・・・・・・・
     ---------------
    """
    data = sp.genfromtxt(csv_file, delimiter=",")
    x = data[:, 0]
    y = data[:, 1]
    """
    ↑のように書くと、
    x = [1, 2, 3, ・・・]
    y = [1, 10, 100, ・・・]
    のように、CSVファイルの列のデータを取り出すことができます。
    便利。
    """
    """
    データをプロットします。
    """
    plt.scatter(x, y)
    """
    lavelは自由に変更しても構いません。
    """
    plt.xlabel("カウント")
    plt.ylabel("実データ")
    """
    グラフを表示するときのスケールを設定できます。
    """
    plt.autoscale(tight=True)
    """
    プロットされたグラフを表示します。
    """
    plt.show()
if __name__ == '__main__':
    plot_data("./access_data.csv")

curve_fitting.pyを実行してみます。

python curve_fitting.py

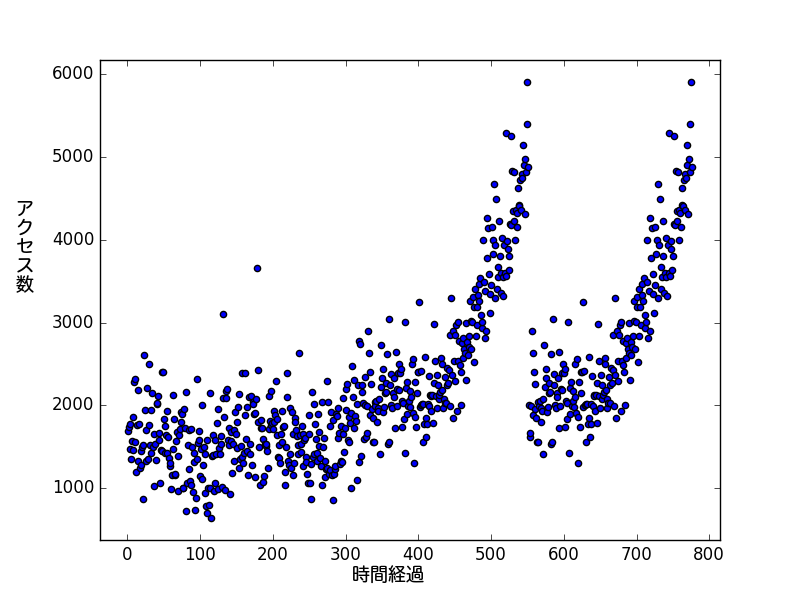
データがプロットされました。突然アクセス数が落ちているのはなぜでしょうか。もしくは逆に急激に上がっているのか・・・炎上・・・？
などと邪推せずに、曲線フィッティングを行ってみます。曲線フィッティングは「curve_fitting2.py」を実行します。

# -*- coding; utf-8 -*-
import os
import matplotlib.pyplot as plt
import scipy as sp
def plot_data(csv_file):
    """
    データをプロットする関数
    csv_file:
    以下のような形式のCSVファイル
    ---------------
    1,1
    2,10
    3,100
    ・・・・・・・・
     ---------------
    """
    data = sp.genfromtxt(csv_file, delimiter=",")
    x = data[:, 0]
    y = data[:, 1]
    """
    ↑のように書くと、
    x = [1, 2, 3, ・・・]
    y = [1, 10, 100, ・・・]
    のように、CSVファイルの列のデータを取り出すことができます。
    便利。
    """
    """
    データをプロットします。
    """
    plt.scatter(x, y)
    """
    曲線フィッティングを描画します。
    scipyで曲線フィッティングしてくれるpolyfitという関数があります。
    polyfit とは、 polynomial fitting の略で、polinomial とは「多項式」のことなので、
    厳密には多項式フィッティングというべきでしょうか。
    色々な値が返ってきますが、aの中に多項式の説明のところにあるa_0、a_1、・・・のデータが入っているので、aだけを使います。
    dim の数を増やすことで、曲線の波の個数が増えていきます。
    """
    dim = 10
    a, residuals, rank, sv, rcond = sp.polyfit(x, y, dim, full=True)
    """
    aを使って、曲線（多項式）を求めます。
    """
    f = sp.poly1d(a)
    """
    多項式を描画します。
    描画する横軸xの範囲を指定(fx)し、描画します。
    """
    fx = sp.linspace(0, x[-1], 1000)
    plt.plot(fx, f(fx), "r", linewidth=6)
    """
    lavelは自由に変更しても構いません。
    """
    plt.xlabel("カウント")
    plt.ylabel("実データ")
    """
    グラフを表示するときのスケールを設定できます。
    """
    plt.autoscale(tight=True)
    """
    プロットされたグラフを表示します。
    """
    plt.show()
if __name__ == '__main__':
    plot_data("./access_data.csv")

python curve_fitting2.py

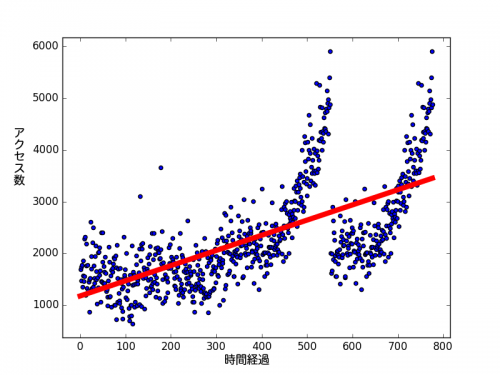
赤い線が一本出ました。なんとなくデータに従って上向きに上昇しているようですが、いまいちです。しかも曲線ではありません。
なぜ曲線でないかというと、「curve_fitting2.py」の53行目が

    dim = 1

となっているからです。dimという値は、上の多項式のnの値です。dim=1の場合、曲線の多項式fは

となり、これは直線の式です。ではdim=2にして再度実行してみます。

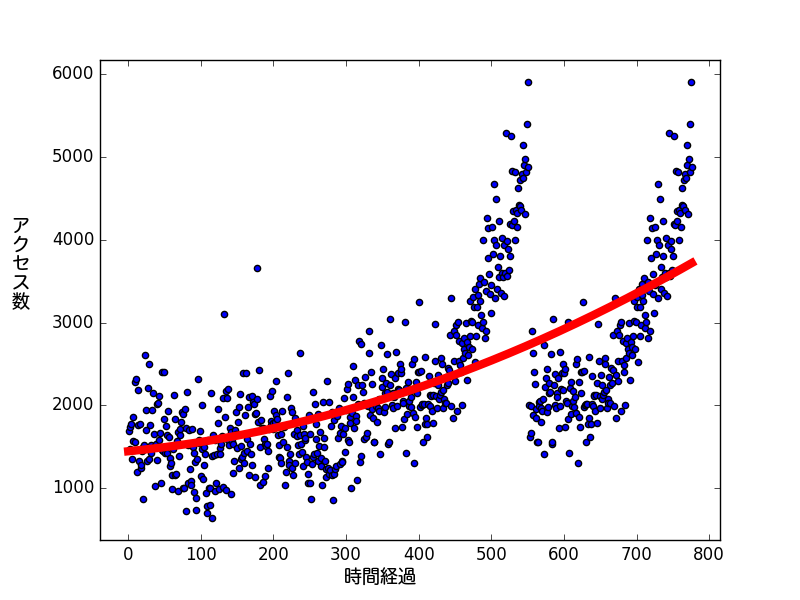
ゆるやかですが、少し曲がった線になりました。先程よりデータに沿った線になっていますね。
ではdimをもっと上げてみたら・・・お試し下さい。
上のソースコードのコメントでも書いてある通り、曲線フィッティングは「sp.polyfit」という関数で行っています。
次回は、この「sp.polyfit」がどのようにして曲線フィッティングを実現しているかをご紹介します。