検索

ARモデルの表現能力を考察する

tmtk

その他

2019.3.1

Topics

こんにちは。データサイエンスチームのtmtkです。
この記事では、ARモデルの表現能力について考察します。

はじめに

前回までの記事では、時系列解析の入門としてARモデルについて紹介し、AICによるARモデルのモデル選択について解説しました。
この記事では、ARモデルの表現能力について考察します。
ニューラルネットワークの理論では、Universal Approximation Thorem（普遍近似定理）が有名です。これは、「任意の連続写像 f \colon [0, 1] ^ n \to \mathbb{R}は、隠れ層が1層のニューラルネットワークで任意の精度で近似できる（隠れ層のユニットを十分多くすれば）」という内容の定理です。標語的にいえば、隠れ層が1層のニューラルネットワークモデルは無限の表現能力（Representational capacity）をもつ、といえると思います。この定理のおかげで、機械学習モデルを作りたいとき、ほしいモデルは隠れ層が1層のニューラルネットワークで表現できることがわかります。隠れ層が1層のニューラルネットワークを訓練して思うような性能が出ない場合、隠れ層のユニット数が足りないか、最適化に失敗しているかのどちらかだという考察ができます。普遍近似定理が与える洞察によって、問題の切り分けができるわけです。
そこで、ARモデルの場合にも、モデルの表現能力について考察します。

ARモデルの表現能力

ARモデルは、式

y_t = \sum_{i = 1}^m a_i y_{t - i} + v_t \quad (t = m + 1, \ldots, N)
で与えられるのでした。このモデルには正規分布にしたがう誤差項v_tが含まれているため、どんなデータ\{y_t\}_{t=1}^NでもARモデルの実現値とみなすことができます。そのため、ここでは誤差項をなくした式

y_t = \sum_{i = 1}^m a_i y_{t-1} \quad (t = m + 1, \ldots, N)
で表現されるデータ\{y_t\}_{t = 1}^Nについて調べます。

結論

結論からいってしまうと、漸化式y_t = \sum_{i = 1}^m a_i y_{t-1} \quad (t = m + 1, \ldots, N)を満たす数列\{y_t\}の空間についてはよく知られており、以下のようになります。漸化式の特性方程式

x^m - \sum_{i=1}^m a_i x^{m - i} = 0
が複素数上で相異なる解\lambda_1, \ldots, \lambda_kと自然数（重複度）d_1, \ldots, d_kを用いて

(x - \lambda_1)^{d_1}\dots (x - \lambda_{k})^{d_k} = 0
と因数分解されるとき、

y_t = t^a \lambda_i ^ t \quad (0 \leq a \leq d_i - 1)
の形の数列の一次結合全体が漸化式の解\{y_t\}_t全体になります。（参考文献を参照のこと）

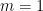例：次数m=1の場合

ここからは具体例を見ていきます。
次数m=1の場合は、漸化式は

y_t = a_1 y_{t-1}
となります。これはよく知られているように、等比数列をあらわす漸化式で、一般解は

y_t = a_1^{t-1}y_1
となります。したがって、次数m=1の場合は、ARモデルは等比数列（と誤差項の和）をモデリングしていることになります。

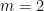例：次数m = 2の場合

もう少し複雑な例として、次数がm=2の場合について考察します。この場合、漸化式は

y_t = a_1 y_{t-1} + a_2 y_{t-2}
となります。一般解は、c_1, c_2をy_1, y_2から決まる定数として、

y_t = c_1 \lambda_1^t + c_2 \lambda_2^t
または

y_t = c_1 \lambda_1^t + c_2t\lambda_1^t
となります。次数m=1の場合と似ていますが、m=2の場合に起こる興味深いこととして、サインカーブや直線を表せるようになるということがあります。実際、サインカーブについては

y_t = \sin(at)
で数列\{y_t\}_tを定めると、これは漸化式

y_{t} = 2\cos a y_{t-1} - y_{t-2}
を満たします。そのため、次数m=2のARモデルは、サインカーブを誤差0で表すことができます。このようにサインカーブがARモデルで表現できる背景としては、オイラーの公式

e^{i\theta} = \cos\theta + i\sin\theta
があります。オイラーの公式より、サイン関数が

\sin x = \frac{e^{ix} - e^{-ix}}{2i}
と、指数関数（等比数列）の和で表せるため、サインカーブが2次のARモデルの形で表現できるのです。また、直線については、

y_t = at + b
で数列\{y_t\}_tを定めると、これは漸化式

y_{t} = 2y_{t-1} - y_{t-2}
を満たします。そのため、次数m=2のARモデルは、直線を誤差0で表すことができます。前に述べた漸化式の一般論の立場からみると、この漸化式の特性方程式は

x^2 = 2x - 1
であり、x = 1に2重解をもっています。そのため、漸化式 y_{t} = 2y_{t-1} - y_{t-2}の一般解は、定数c_1, c_2を用いて

\begin{aligned} y_t & = c_1 1^t + c_2 t 1^t \\ & = c_1 + c_2 t\end{aligned}
となり、これは直線の方程式です。

以上から、ARモデルは、多項式関数、指数関数、三角関数を掛け合わせたり足し合わせたりしたようなデータを表現するのに向いている、ということがいえそうです。

まとめ

この記事では、ARモデルの表現能力をみるため、ARモデルから誤差項をとりのぞいた漸化式の解空間について考察しました。
以上から、ARモデルは、多項式関数、指数関数、三角関数を掛け合わせたり足し合わせたりしたようなデータを表現するのに向いている、ということがいえそうです。

参考文献

テックブログ新着情報のほか、AWSやGoogle Cloudに関するお役立ち情報を配信中！

tmtk

データ分析と機械学習とソフトウェア開発をしています。 アルゴリズムとデータ構造が好きです。

Recommends

こちらもおすすめ

Special Topics

注目記事はこちら

これから始めるBigQuery基礎知識

データ分析入門
これから始めるBigQuery基礎知識

2024.02.28

ホワイトペーパー

AWSの請求代行リセールサービス

　AWSの料金が 10 %割引になる！
『AWSの請求代行リセールサービス』

2024.07.16

サービス