基礎からはじめる時系列解析入門
こんにちは。データサイエンスチームのtmtkです。
この記事では、時系列解析で使われるARモデルについて、基礎から解説します。
ARモデルとは
ARモデルというのは、時系列のデータ に対して、
ARモデルのパラメータ推定
ARモデルのパラメータのうち、
は最尤推定により推定することができます。残りのパラメータ
の選択にはAICが使われますが、ここでは解説しません。
尤度関数は
Pythonでモデリングしてみる
それでは、実際にPython 3でARモデルを使ってみます。
Pythonでは、StatsModelsというパッケージでARモデルが提供されていますが、ここではARモデルが多変数の線形回帰モデルと同一視できることを活かして、scikit-learnの線形回帰モデルを使ってみることにします。なお、上の説明で添え字が1-originだったのとは異なり、Pythonでは添え字が0-originであることに注意します。
まずは必要なライブラリをインポートします。
import numpy as np from sklearn.linear_model import LinearRegression np.random.seed(1234)
次に、コサインカーブに正規分布によるノイズを加えた、サンプルサイズ200の時系列データセットを作成します。
N = 200 std = 0.3 x = np.arange(0, N) y = np.cos(x*np.pi/10) + np.random.normal(0, std, N)
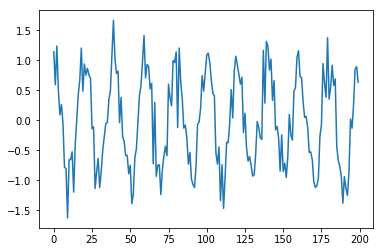
今回は次のARモデルを構築することにします。線形回帰を実行するため、データを整形します。
と
を作成します。
m = 20
X = np.zeros((N - m, m))
for i in range(N - m):
X[i] = y[i: i + m][::-1]
Y = y[m:]
最後に、パラメータの推定を行います。普通の線形回帰モデルと異なり、切片がモデルに含まれていないことに注意します。
lr = LinearRegression(fit_intercept=False) lr.fit(X, Y)
これでARモデルのパラメータの学習が完了します。ARモデルの式
y_predictedとして計算します。
prediction_len = 100
y_predicted = y
for i in range(prediction_len):
t = [y_predicted[-m:][::-1]]
y_predicted = np.append(y_predicted, [lr.predict(t)[0]])
y_predicted = y_predicted[N:]
すると、以下のように未来の値を予測ができていることがわかります。
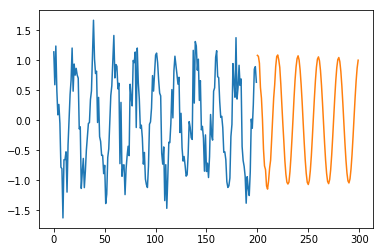
まとめ
この記事では、時系列解析の入門として、ARモデルを紹介しました。ARモデルのパラメータ推定の方法や線形回帰との関係について説明し、Python 3で実際にARモデルの学習と予測を行いました。
次回の記事では、AICによるパラメータの選択について解説します。
参考文献
- 樋口知之『予測にいかす統計モデリングの基本―ベイズ統計入門から応用まで』
- 北川源四郎『時系列解析入門』
- 線形回帰 – Wikipedia
テックブログ新着情報のほか、AWSやGoogle Cloudに関するお役立ち情報を配信中!
Follow @twitterデータ分析と機械学習とソフトウェア開発をしています。 アルゴリズムとデータ構造が好きです。
Recommends
こちらもおすすめ
-

ARモデルの表現能力を考察する
2019.3.1
-

AICによるARモデルのモデル選択
2019.2.28
-

ARモデルの誤差分析について
2019.3.7
-

口コミデータを活用したレコメンドシステムの可能性
2017.12.7
Special Topics
注目記事はこちら

データ分析入門
これから始めるBigQuery基礎知識
2024.02.28

AWSの料金が 10 %割引になる!
『AWSの請求代行リセールサービス』
2024.07.16



