ARモデルの誤差分析について

Topics
こんにちは。データサイエンスチームもtmtkです。
この記事では、ARモデルの誤差分析について説明します。
はじめに
前の3回の記事にわたって、時系列解析の入門としてARモデルについて紹介し、AICによるARモデルのモデル選択について解説し、ARモデルの表現能力について議論しました。
ARモデルをつかうと過去の時系列データから未来のデータの値を予測することができます。実際に予測を行う場合には、その予測の信頼区間も知りたいことが多いと思います。つまり、予測がどれくらいずれうるのかまでを知りたいということです。
この記事では、ARモデルで未来のデータを予測するとき、予測の誤差について考察します。
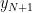 の誤差分析
の誤差分析
ARモデルは、式
で表され、誤差項
そのため、いま、過去のデータ
データ分析を実際にする状況では、誤差項
ただし、この記事では、今後の計算を簡単にするため、以下では
一般の場合(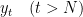 )の誤差分析
)の誤差分析
時刻での
の予測値を表す数列を、
とおきます。いま、過去のデータ
が与えられているとします。すると、
の範囲では観測値
が与えられているため、予測値
は
とおくことができます。
未来の時刻に対しては、ARモデルとそれまでの推定値
から
と計算することができます。
未来の時刻に対して、予測誤差
のしたがう分布を考えてみましょう。前の議論から、
のときは
に従うのでした。次に
の場合を考えます。すると、
これまで時刻
以上より、
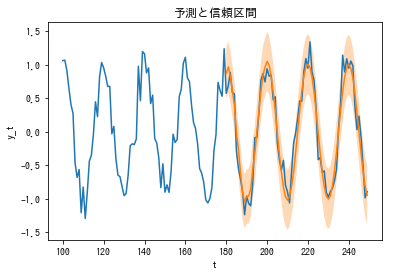
(真の値、予測値、95%信頼区間をプロットしたもの)
まとめ
この記事では、ARモデルの予測の信頼区間を計算しました。ただし、計算にあたって簡単のため誤差項の母分散
が既知であることを仮定しました。
参考文献
- 北川源四郎『時系列解析入門』
テックブログ新着情報のほか、AWSやGoogle Cloudに関するお役立ち情報を配信中!
Follow @twitterデータ分析と機械学習とソフトウェア開発をしています。 アルゴリズムとデータ構造が好きです。
Recommends
こちらもおすすめ
-

AICによるARモデルのモデル選択
2019.2.28
-

ARモデルの表現能力を考察する
2019.3.1
-

基礎からはじめる時系列解析入門
2019.2.22
-

機械学習の受託案件を通じて気づいた5つのこと
2019.3.8
-

社内マッサージルーム利用状況がパレートの法則にしたがっているかを検証する
2018.9.26
Special Topics
注目記事はこちら

データ分析入門
これから始めるBigQuery基礎知識
2024.02.28

AWSの料金が 10 %割引になる!
『AWSの請求代行リセールサービス』
2024.07.16
