こんにちは。データサイエンスチームのtmtkです。
この記事では、AICによるARモデルのモデル選択について説明します。

背景

前回の記事では、時系列解析の入門としてARモデルを紹介しました。そこでは、パラメータのうち次数の推定という課題が残っていました。
次数は増やせば増やすほど、既存のデータに対する適合性はあがりますが、増やしすぎると未知のデータに対する予測性能が悪くなることが知られています。この現象は過学習や過適合とよばれます。
AIC（An Information CriterionまたはAkaike Information Criterion、赤池情報量規準）というのはARモデルの“ちょうどいい”次数を見つけるのに使える指標です。

AICとは

AICについての詳細は各種書籍にゆずることにし、ここでは簡単に定義と結論だけ述べます。
AICは

で定義されます。ここで、変数はモデルのパラメータ、はの最尤推定量、関数は対数尤度関数、はモデルのパラメータの数です。
は平均対数尤度の近似的な推定量になっているため、を最小にする次数を選択することで、最適なモデルを選ぶことができるとされています。

ARモデルのAIC

それでは、実際にARモデルのAICを計算し、最適なモデル選択をしてみます。
データとして、コサインカーブに正規分布ノイズを加えたデータを使います。

import numpy as np
np.random.seed(1234)
N = 200
std = 0.2
x = np.arange(0, N)
y = np.cos(x*np.pi/10) + np.random.normal(0, std, N)

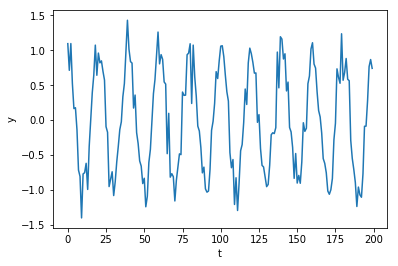
200個のサンプルのうち、最後の20個のサンプルはテスト用データセットとしてホールドアウトしておき、残りの180個のデータに対し、ARモデルを作成します。次数を1から50まで変化させたとき、AICは以下のように変化します。

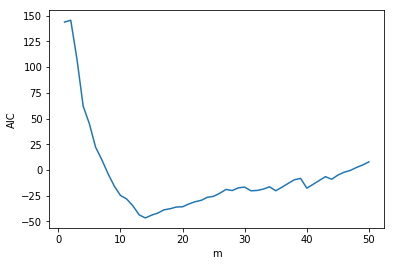
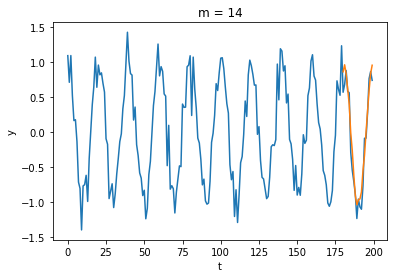
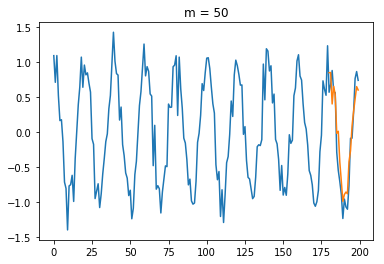
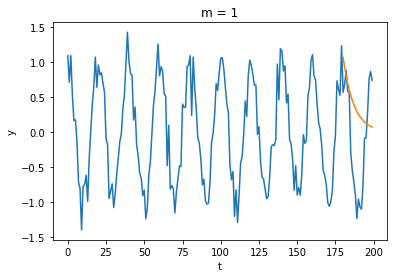
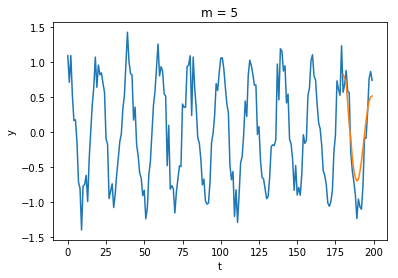
次数のモデルがAIC最小を達成するモデルだとわかります。次数がそれぞれの場合に対して、とARモデルからを推定したものをプロットしてみます。の場合とくらべると、明らかにの場合はよいモデルになっていることがわかります。

AICとホールドアウト法

以上で、AICによるARモデルの選択を説明しました。機械学習の文脈では、モデル選択の方法として、ホールドアウト法やそれを発展させた交差検証法（Cross Validation）がよく使われていると思います。そこで、AICによるモデル選択と、ホールドアウト法によるモデル選択の関係を実験的に調べてみます。
上の実験と同様の状況で、各次数に対するAICと平均二乗誤差（Mean Squared Error）の関係を調べます。平均二乗誤差は、からARモデルで予測したと、実際のを比べて計算します。
AICと平均二乗誤差をプロットすると、以下のようになります。

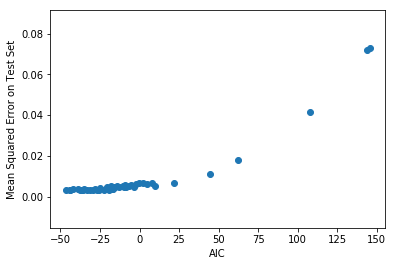
AICが小さくなるほど平均二乗誤差も小さくなる傾向を読み取ることができます。したがって、この場合はAIC最小のモデルを選ぶことと、ホールドアウトしたデータセットに対する平均二乗誤差が最小になるモデルを選ぶことは、おおむね同じことになります。

まとめ

この記事では、AICを説明し、AICを使ってARモデルの次数選択を行いました。
また、AICが小さいモデルほど、予測誤差が小さくなる傾向を、実験的に確認しました。

参考文献

• 北川源四郎『時系列解析入門』
• 坂元慶行・石黒真木夫・北川源四郎『情報量統計学』
• 信号解析　第８回講義録