機械学習曲線フィッテングについて　後編

編集部

Data Science

2016.4.13

Topics

曲線フィッティングのメリット・デメリット
誤差関数
実際にコードで書いてみる
次回予告

一ヶ月ぶりの更新となってしまいました。
橘です。
今後しばらくはペースアップを図って行きます！
さて、前回は曲線フィッティングをを実際に見ていきました。
前回までの内容をざっとまとめると、

目的は、「過去のデータにフィットするような曲線を引き、新たなデータを予測したい
曲線は、多項式 $f(x) = \sum_{i=0}^{n} w_{ i} x^{i}$ で表すことができる
多項式のnの値を増やすことで、曲線をたくさん曲げることができ、より過去のデータにフィットした線を引くことができる

というものでした。
今回は曲線フィッティングのメリット・デメリットと数学的背景をご紹介します。

曲線フィッティングのメリット・デメリット

曲線フィッティングのメリットをさらっと挙げると

機械学習で使われる手法の中では比較的簡単に実装できる
簡単な割には使われる場面が多い

という点です。しかし、どちらかというとデメリットの方が重要です。

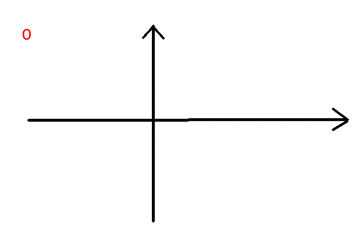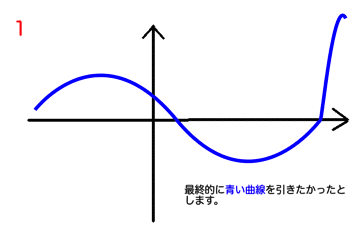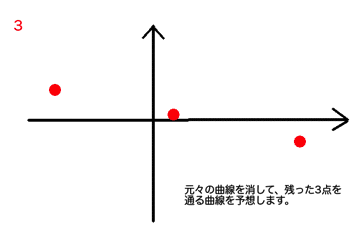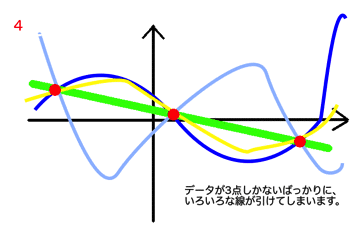
データが少ないと思うように予測できるいい曲線が引けない
不用意に多項式のnを増やし過ぎると過学習が起こる
曲線の係数{ $w_{i}$ }を求める計算に時間がかかる

１つずつ説明していきます。

1. データが少ないと思うように予測できるいい曲線が引けない

次のGIFアニメをご覧ください。

元々予測したいデータの個数が少ないと、曲線の引き方がかなり自由になってしまい、思ったような曲線を引くことができなくなってしまいます。
これは機械学習全般にいえることですが、データは多いにこしたことはありません。

2. 不用意に多項式のn を増やし過ぎると過学習が起こる

詳細は後ほどの数学的背景で述べますが、前回と今回の冒頭でご説明した通り、多項式のnを増やすことで曲線の曲げる数を増やすことができます。であれば増やせば増やすほどよさそうなものですが、「過ぎたるは及ばざるが如し」で、過学習と呼ばれる現象が起こります。
過学習とは、「1. データが少ないと思うように予測できるいい曲線が引けない」ではデータの個数が少なすぎて曲線が自由になってしまいましたが、
その逆で曲線を曲げる回数を増やしすぎることで、曲線が束縛されてしまう起こる現象です。
またGIFアニメで見てみましょう。

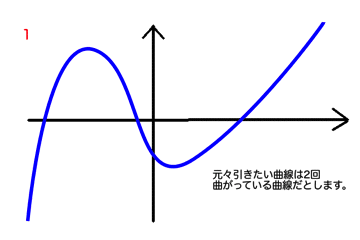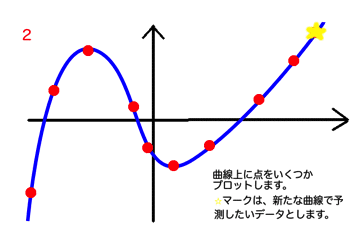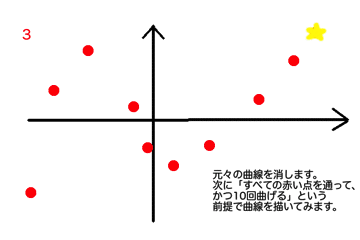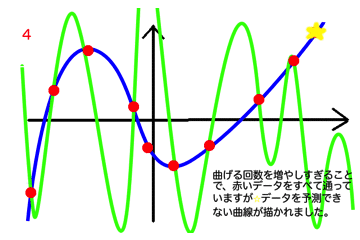
曲げる回数に束縛されてしまい、予測したいデータが予測できないことがわかるかと思います。データがたくさんある場合、なるべく多くのデータを通るような曲線を描きたくなりますが、多ければいいというものではありません。適切なnを見つけることが大事です。
「3. 計算量が増えてしまう」に関しては、数学的背景でご紹介することにします。

曲線フィッティングの数学的背景について

ここからやっと、数学の話です。前にご紹介した微分の話や行列の話を復習しつつ、ご紹介していきます。

曲線

曲線に関しては、今まで通りの多項式で表していきます。
$f(x) = \sum_{i=0}^{n} a_{i} x^{i}$

誤差関数

曲線フィッティングのそもそもの目的を今一度思い出すと、目的に焦点を絞れば
(i) 適当な $\{w_{i}\}_{i=0}^{n}$ を決めて曲線 $f(x) = \sum_{i=0}^{n} w_{ i} x^{i}$ を引く
(ii) 過去のデータから計算して、曲線の係数{ $w_{i}$ } を決める
(iii) (ii)で決めたa_{i}を曲線の多項式に代入して曲線を変形させる
でした。(くどいようですが、多項式に不安を感じる方は機械学習を学ぶための準備その2（級数と積分について）をご覧ください。)
(i)で適当な $\{a_{i}\}_{i=0}^{n}$ を決めて(ii)で曲線とフィットさせていきます。次の図のようなイメージです。

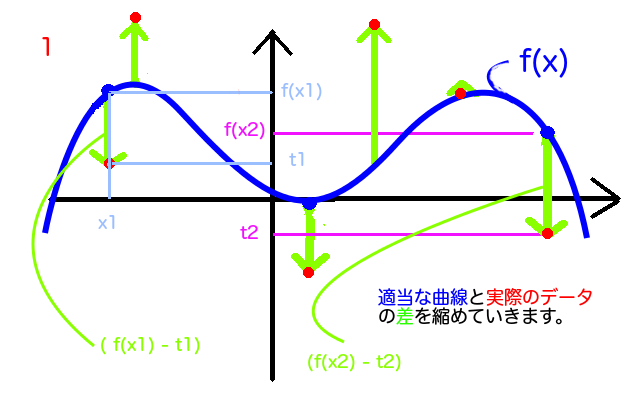
ごちゃごちゃしていますが、「実データ(赤)のy座標 $(t_{1}, t_{2})$ 」と、
実データの真上か真下にある曲線のy座標 $(f(x_{1}), f(x_{2}))$ の差が、そのx座標における実データと曲線との「誤差」です。
M個のデータに関してそれぞれの誤差を二乗して足しあわせたものが「誤差関数」、今回の場合は「二乗誤差」といいます。なぜ二乗するかというと、実データと曲線がどちらが上にあるかによって誤差がプラス/マイナスが反転してしまうため、誤差をプラスにそろえるために2乗します。最後に、あとで計算を楽にするために、すべての誤差を足しあわせたものを2で割ります。
$E_{D} = \frac{1}{2} \sum_{m=1}^{M} \{f(x_m) - t_{m}\}^{2}$
上の図で見たように、ただ「データと曲線にどれだけ差があるか」を見ているにすぎません。
$E_{D}$ の中にある $f(x_{m})$ はそもそも
$f(x) = \sum_{i=0}^{n} w_{i} x^{i}$
という形でした。これを $E_{D}$ に代入します。
$E_{D} = \frac{1}{2} \sum_{m=1}^{M} \{\sum_{i=0}^{n} w_{i} x_{m}^{i} - t_{m}\}^{2}$
$E_{D}$ は「誤差」なので、なるべく小さい方がいいような気がします。今回、誤差関数の中には $x_{m}$ や $t_{m}$ や $w_{i}$ などの数が入っていますが、今回我々が数値を変更することのできるのは $w_{i}$ だけです。なぜかというと、xとtの値は実データのx座標とy座標であり、定まった値です。そしてwはそもそも、曲線を描くために適当に決めたものでした。ですので、この誤差関数の全体が小さくなるような、 $w_{i}$ を計算していきます。
さて、遡ること4ヶ月前、当テックブログで微分について書きました。そこで
「関数がある点で最大値、もしくは最小値を取るとき、その点で微分した値は0になる」
という事実についてお話ししました。上の事実を適用すると、
「誤差関数がある $w_{i}$ で最小値をとるとき、誤差関数を $w_{i}$ で微分した値は0になる」
ということになります。この事実を使うことで、誤差関数が最も小さくなる $w_{i}$ が求められます。
今回は、 $\{w_{i}\}$ をどのように求めればいいかのところまでにし、次回はその証明と数式をコードに落とし込む方法をおまけ編として公開する予定です。

誤差関数が最小となる曲線の係数wの求め方

いきなり行列が出てきていたりしていますが、以下がwの求め方です。

一見複雑に見えますが、実際に複雑です。。。が、計算結果だけを求めたいのであれば、前回利用したPythonのscikit-learnライブラリを使うことで、wの値をすぐに求めることができます。このwの値を取得することで、ようやく曲線を描くことができます。

実際にコードで書いてみる

前回はscikit-learnライブラリで結果だけを求めましたが、今回は自力で最小二乗法による曲線フィッティングを書いてみました。上述の通り、コードの具体的な説明は次回行います。
umentu/least_square
※ソースコードの改変、再配布は認めますが、一切の責任は持たないことをご了承して頂いた上でご利用下さい。
環境に関しては、前回の通りこちらをごらんください。また、わからない場合はFacebookでお気軽にご相談ください。

#! -*- coding: utf-8 -*-
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
from pandas import Series, DataFrame
from numpy.random import normal
def create_dataset(tsv):
    data_set = DataFrame(columns=["x", "t"])
    data = sp.genfromtxt(tsv, delimiter=",")
    for d in data:
        data_set = data_set.append(Series(d, index=["x", "t"]),ignore_index=True)
    return data_set
def least_square(dataset, n):
    """
    最小二乗法で解を求める
    """
    # phi を求める
    phi = DataFrame()
    for i in range(0,n+1):
        p = dataset.x**i
        p.name = "x**{0}".format(i)
        phi = pd.concat([phi,p], axis=1)
    w = np.dot(np.dot(np.linalg.inv(np.dot(phi.T, phi)), phi.T), dataset.t)
    def f(x):
        y = 0
        for i, wt in enumerate(w):
            y += wt * (x ** i)
        return y
    return (f, w)
if __name__ == '__main__':
    # 訓練データ作成
    train_data = create_dataset("./access_data.csv")
    # テストデータ作成
    test_data = create_dataset("./access_data.csv")
    N = 5
    (f, w) = least_square(train_data, N)
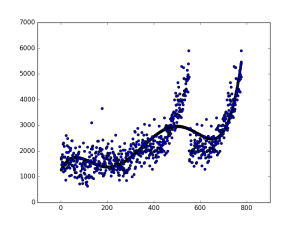
    plt.scatter(test_data.x, f(test_data.x))
    plt.scatter(test_data.x, test_data.t)
    plt.show()

以下がコードの実行結果です。