「21世紀の相関係数」を超える

この記事は#DataScience by DATAHOTEL Tech blog Advent Calendar 2017の10日目の記事です.
はじめに
我々のチームでは,データを分析するために色々な機械学習の手法を使っています.
この記事では教師無し機械学習と呼ばれるデータマイニング手法を取り上げます.すなわち,教師データ(ラベル付きデータ)が無くても,データから何かのパターンや特徴を読み取る手法で,クラスタリングや特徴抽出が代表的なジャンルとされています.
関連性を考える
古くから存在する機械学習(という言葉が無かったはるか昔から)の手法の一つに,複数のデータの間の関連性を推定する相関関係推定があります.データからの特徴抽出と言って良いでしょう.より具体的には,2変数間の関連性を推定するピアソンの相関係数があります.
ピアソンの相関係数には,次のような思想があります.
通常使われる相関係数:2つの変数において,スカラー値が以下のような値を持つ
- 片方が増加するともう片方も増加する場合,増加の度合いに応じて絶対値が1以下の正の値を取る
- 片方が増加するともう片方は減少する場合,増加の度合いに応じて絶対値が1以下の負の値を取る
- 片方が増加してももう片方は変化しない場合,ゼロとなる
データ系列が線形(直線関係)にあることが仮定されているために,非線形,つまり曲線の関係にある2変数の関連性はほとんど計算することができません.
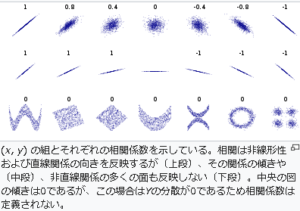
Wikipediaでも最初に図示されています
ピアソンの相関係数は,与えられた沢山の2次元データ
相関係数は以下の式で計算され,データ系列
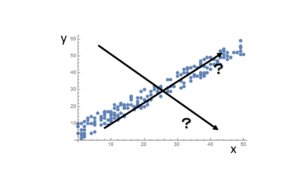
ところが,直線をどうやって引いたら良いか分からない場合,人間の直感とは異なる値が計算されます.
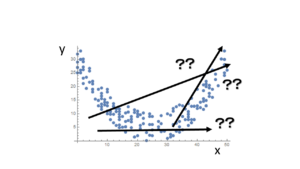
図のような2次関数の場合は,ピアソンの相関係数はゼロに近くなります.つまり点のと
の関係は無いと判断されるのですが,本当は関係が無いどころか二次関数の関係があります.
そこで各問題ごとに色々な手法を使って相関関係を調べるのですが(局所的に相関係数を計算するなど),一般的に解決しようと提案された手法の一つが「21世紀の相関」と紹介されたthe maximal information coefficient (MIC)です.
MICには,ピアソンの相関係数とは違う思想があります.
MIC:2つの変数において,スカラー値が以下のような値を持つ
- ある領域の中で2変数の値の相互情報量に応じた正の値を取る
- 2変数の値域の中での分布が一様分布に近づくほど値はゼロに近づく
ここで出て来る(データのx座標とy座標が必ずペアで観測されるという仮定の元での)相互情報量は以下の式で定義され,やはりデータ系列が具体的に与えられると,実際の値を計算することができます.
この相互情報量が最大となる状態をグリッドサーチするわけですが,イメージは素晴らしいスライドを作ってくれた方がおられるのでご参照下さい.
21世紀の手法対決 (MIC vs HSIC)
ところが,MICは素晴らしいのですが,使っているといくつか解決したい点も感じてきます.
- 多重解像度で各解像度毎に相互情報量を計算しながらグリッドサーチをするので,計算量が多い
- 疑似相関にひっかかる
そこで,MICの思想を受け継ぎながらも異なるアプローチで開発したものが,テコラスデータサイエンスチームで開発した確率モデルに基づき多重解像度解析を行わずに局所的及び大局的な情報量を考慮して相関を計算するR-AMIC(Resampling based Approximated Mutual Information Coefficient)です.
R-AMICは,以下の思想に基づき設計されています.
R-AMIC:2つの変数において,スカラー値が以下のような値を持つ
- ある領域の中で2変数の値の相互情報量に応じた正の値を取る
- 2変数の値域の中での分布が一様分布から離れるほど値は大きくなる
このうち一つ目は,データ系列に対して相互情報量を計算するだけなのでMICと同じです.二つ目の意味を説明します.
まず,平面上に乱数を用いて一様分布を発生させます.
次にデータ系列からデータを入力し,分布を再サンプリングします.これにより,グリッドサーチをしなくても,ある領域にデータが存在する確率を(近似的に)計算することができます.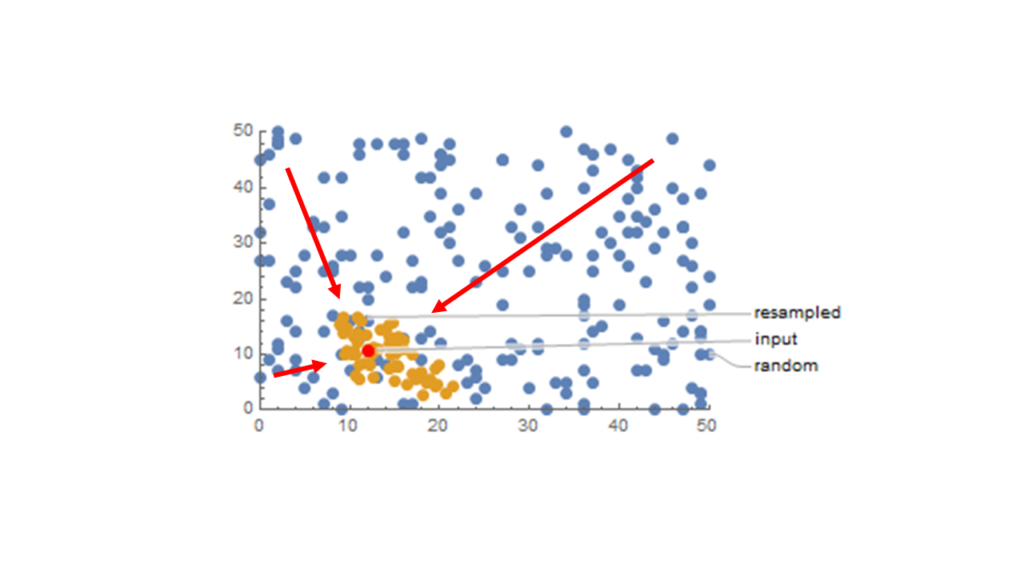
データ系列から順にデータを取り出し再サンプリングすることを繰り返すと,相互情報量を計算するための確率密度マップを作成できます.
直線に対しては次のようなものができます.
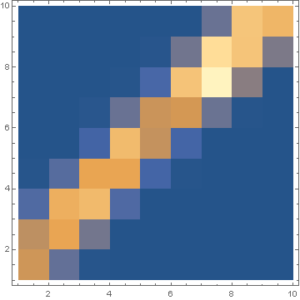
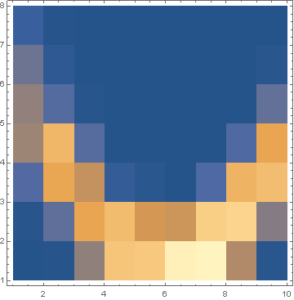
線形ではない2次関数の場合は,次のような確率密度マップができます.
各データの確率密度が分かれば相互情報量を計算することができ,相関係数が計算できます.
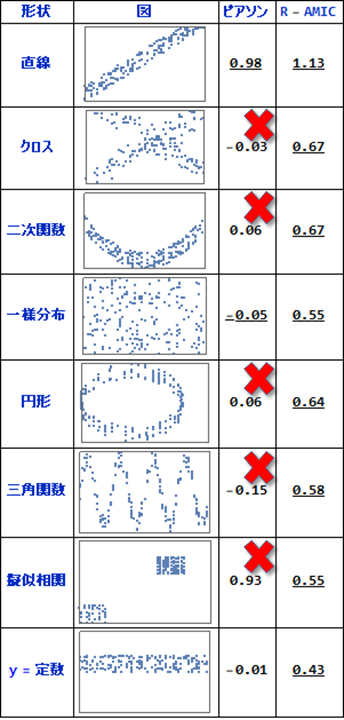
いくつかのデータ系列に対し,ピアソンの相関係数とR-AMICを計算した結果が以下です.
今回の計算では,R-AMICの値は正規化せれていず,R-AMICの値同士の比較に意味があることに御注意下さい.
上から順に見ていきます.
直線では,どちらの計算方法でも高い相関があると出ています.
しかしクロスでは,人間が見るとクロス状のパターンが見て取れるにも関わらず,ピアソンの相関係数はゼロに近く,関連性は見いだせていません.二次関数も同様です.
x座標y座標ともにランダムな一様分布により作成されたデータでは,どちらの手法でも値が小さく,関連性が無いことが示唆されています.R-AMICの値はピアソンの相関係数に比べると大きな値ですが,R-AMICは正規化せれていずR-AMIC同士の値の大きさの比較に意味があることを再考下さい.
円形及び三角関数の場合は,ピアソンの相関係数では値がゼロに近く関連性が無いことになりますが,R-AMICでは関連性を示しています.
擬似相関は.2つのランダムな一様分布によるデータで,乱数なので関連性はありません.ところがピアソンの相関係数では,直線に近い関連性を示しています.このケースは,MICでも検出に失敗することが指摘されています.R-AMICでは上から4番目の一様分布の場合と同じ値で,関連性が無いことが検出できています.
y=定数は変化が無いので関連性は無く,どちらの値も関連性が無いことを検出できています.
おわりに
人間が見てなんとなく関連がありそうだなぁと思えるものに対し,それらしい相関値を計算する手法を紹介致しました.非線形のパターンは無限にありいくつかの例しか紹介できませんでしたが,直感に即するような値が計算されていました.
紹介した実験はMathematicaを使ったもので,R-AMICの正規化もされておりませんしMICとの比較も行っておりません.
改良点もまだまだあり,ピアソンの相関係数に比べると相互情報量の計算や再サンプリングの計算は依然として計算コストが高いです.ただしどちらも情報理論・機械学習・統計や物理の分野で大量の研究がありいくらでも改善の余地があります.
ピアソン以外の相関係数やMIC以外非線形系用相関係数との比較も行いたいと思いますので,次回を御期待下さい.
テックブログ新着情報のほか、AWSやGoogle Cloudに関するお役立ち情報を配信中!
Follow @twitter大学で民俗学や宗教についてのフィールドワークを楽しんでいたのですが,うっかり新設された結び目理論と幾何学を勉強する研究室に移ってしまい,さらに大学院では一般相対性理論を研究するという迷走した人生を歩んでいます.プログラミングが苦手で勉強中です.
Recommends
こちらもおすすめ
-

Apache Beamのオーバーヘッドについて調べてみた
2017.9.1
-

AWS GlueとAmazon Machine Learningでの予測モデル
2017.12.17
-

NHN FORWARD 2019 参加レポート-AI/機械学習セッションの紹介-
2019.12.4
Special Topics
注目記事はこちら

データ分析入門
これから始めるBigQuery基礎知識
2024.02.28

AWSの料金が 10 %割引になる!
『AWSの請求代行リセールサービス』
2024.07.16