検索

混合ユニグラムモデルについて（トピックモデリング入門）

tmtk

その他

2017.12.18

Topics

　こんにちは。データサイエンスチームのtmtkです。
　この記事では、トピックモデルの一つである、混合ユニグラムモデルについて解説します。
　この記事は、NHN テコラス DATAHOTEL：確率統計・機械学習・ビッグデータを語る Advent Calendar 2017 18日目の記事です。

混合ユニグラムモデルはLDAより単純なトピックモデルです

　混合ユニグラムモデルとは、文書の生成モデルの一つで、トピックモデルに分類されます。
　トピックモデリングで有名なものとして、LDA（Latent Dirichlet Allocation）があります。混合ユニグラムモデルは、LDAに似ていますが、より単純なモデルになっています。LDAと比べると、LDAは一つのドキュメントが複数のトピックを持つのに対して、混合ユニグラムモデルでは一つのドキュメントが一つだけのトピックを持つところが違います。

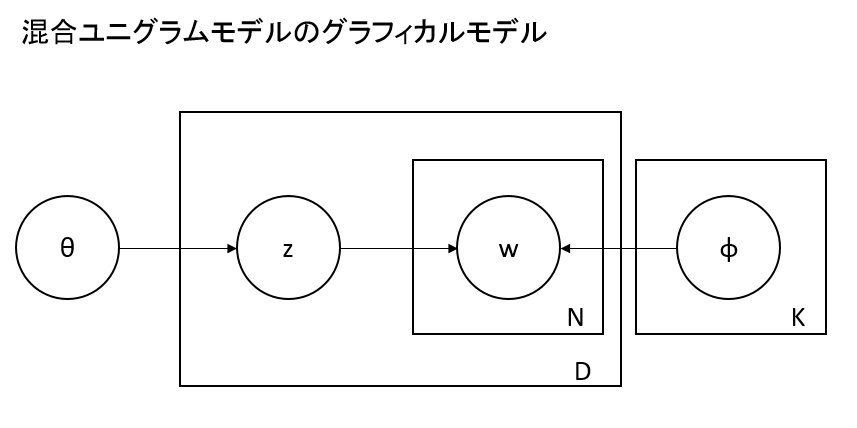
（グラフィカルモデルの読み方については、参考文献をごらんください。また、θ、φの事前分布を仮定し、θ、φがそれぞれ母数α、βに依存する場合もありますが、ここではそれを仮定しないものを解説します。）
　LDAは理解するのが難しいモデルなので、混合ユニグラムモデルはLDAに取り組む前に勉強するモデルにぴったりです。

混合ユニグラムモデルの生成モデル

　混合ユニグラムの生成モデルは、以下のとおりです。具体例をあとで説明しますが、先に形式的に定義します。
　まず、トピック数[latex]K \in \mathbb{N}[/latex]と語彙[latex]\{ w_1, w_2, \ldots, w_V\}[/latex]が与えられているとします。また、トピックの確率分布を定める母数
[latex]\theta = (\theta_1, \theta_2, \ldots, \theta_K) \in \mathbb{R}^K (\theta_k \geq 0, \sum_{k=1}^{K}\theta_k = 1) [/latex]
と語彙の確率分布を定める母数
[latex]\phi = ((\phi_{11}, \ldots, \phi_{1V}), (\phi_{21}, \ldots, \phi_{2V}), \ldots, (\phi_{K1}, \ldots, \phi_{KV})) \in \mathbb{R}^{K\times V} (\phi_{kv} \geq 0, \sum_{v=1}^{V} \phi_{kv} = 1)[/latex]
が与えられているとします。
　このとき、混合ユニグラムモデルによって、ドキュメントは次のように生成されます。

  1. ドキュメントに含まれる語彙の数[latex]N[/latex]を与える。
  2. トピック[latex]k[/latex]をCategorical分布[latex] \mathrm{Categorical}(\theta)[/latex]にしたがって生成する。すなわち、確率[latex]\theta_1[/latex]でトピックを[latex]k=1[/latex]とし、確率[latex]\theta_k[/latex]でトピックを[latex]k=k[/latex]とする。
  3. [latex]N[/latex]個の語彙を、Categorical分布[latex]\mathrm{Categorical}(\phi_k)[/latex]にしたがって生成する。すなわち、確率[latex]\phi_{kv}[/latex]の確率で語彙[latex]w_v[/latex]を選択することを、N回繰り返す。

混合ユニグラムモデルによる生成の具体例

　さきほどの説明を具体的に見てみましょう。
　いま、夏目漱石『吾輩は猫である』と夏目漱石『坊っちゃん』の一部を生成するような混合ユニグラムモデルを考えてみることにします。
　まず、トピック数は[latex]K=2[/latex]として、語彙は{吾輩, 猫, 親譲り, 無鉄砲, 損}（[latex] V= 5[/latex]）とします。
　トピックの分布を[latex]\theta = (0.3, 0.7)[/latex]、語彙の分布を[latex]\phi = ((0.5, 0.5, 0, 0, 0), (0, 0, 0.3, 0.3, 0.4))[/latex]とすることにします。
　そうすると、このパラメータをもつ混合ユニグラムモデルかドキュメントを生成しようとすると、以下のようになります。

  1. ドキュメントに含まれる語彙の数を仮に[latex]N=5[/latex]と定める。
  2. 30%の確率でトピック1が、70%の確率でトピック2が選ばれる。
    • いま、トピック2が選ばれたとする。
  3. トピック2の語彙の分布は(0, 0, 0.3, 0.3, 0.4)なので、{親譲り, 無鉄砲, 損}がそれぞれ(30%, 30%, 40%)の確率で選び出され、それが[latex]N=5[/latex]回繰り返される。
    • 結果は、たとえば「損 損 親譲り 無鉄砲 親譲り」のようなドキュメントが生成される。

混合ユニグラムモデルの学習

　ドキュメントの集合から、混合ユニグラムモデルを学習させることができます。
　学習の方法はいくつか知られていますが、たとえば、EMアルゴリズムというアルゴリズムで学習することができます。EMアルゴリズムは潜在変数（いまの場合はトピック[latex]k[/latex]）をもつモデルによく使われる学習アルゴリズムで、混合ガウスモデルに対する適用が有名だと思います。
　EMアルゴリズムの説明の詳細は省略します。詳細にご興味をお持ちの方は、参考文献をご覧ください。

混合ユニグラムモデルの実装

　混合ユニグラムモデルは、Python3ではたとえば以下のように実装できます。この実装では、形態素解析にMeCabを使用しており、 名詞-一般 に分類された単語のみを語彙（内容語）としてとりあつかっています。また、EMアルゴリズムによる学習も実装しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
""" Unigram Mixture Model. """
__author__ = "tmtk"
import MeCab, random, bisect
class UnigramMixtureModel:
    """A Unigram Mixture Model"""
    def __init__(self, texts, K):
        # The number of topics
        self.K = K
        # extracted contentwords from texts in arguments
        self.contentword_list, self.contentword_dict = self.make_contentword(texts)
        # The number of the vocablary list
        self.V = len(self.contentword_list)
        # parameters of this model
        self.theta, self.phi = self.init_params()
        self.fit(texts)
    # extract content words from texts
    def make_contentword(self, texts):
        m = MeCab.Tagger("-Ochasen")
        contentword_list = []
        for text in texts:
            parsed = m.parse(text)
            words = [word for word in parsed.split("\n") if word not in ['EOS', '']]
            for word in words:
                desc = word.split("\t")
                if desc[3] == "名詞-一般":
                    contentword_list.append(desc[0])
        contentword_list = sorted(set(contentword_list), key=contentword_list.index)
        contentword_dict = {}
        for i, w in enumerate(contentword_list):
            contentword_dict[w] = i
        return contentword_list, contentword_dict
    # calculate parameters by EM algorithm
    def fit(self, texts):
        """EM algorithm"""
        for steps in range(100):
            theta_new = [0]*self.K
            phi_new = [[0]*self.V for _ in range(self.K)]
            for text in texts:
                wordcount = self.calc_wordcount(text)
                for k in range(self.K):
                    q = self.calc_q(text, k)
                    theta_new[k] += q
                    for index in wordcount:
                        phi_new[k][index] += q
            self.theta = L1_normalize(theta_new)
            for k in range(self.K):
                self.phi[k] = L1_normalize(phi_new[k])
    # calclate q for EM algorithm
    def calc_q(self, text, k):
        wordcount = self.calc_wordcount(text)
        numerator = self.theta[k]
        for index in wordcount:
            numerator *= self.phi[k][index]
        denominator_list = []
        for k_ in range(self.K):
            d = self.theta[k_]
            for index in wordcount:
                d *= self.phi[k_][index]
            denominator_list.append(d)
        denominator = sum(denominator_list)
        return numerator/denominator
    # get content words from a text
    def calc_wordcount(self, text):
        m = MeCab.Tagger("-Ochasen")
        parsed = m.parse(text)
        words = [word for word in parsed.split("\n") if word not in ["EOS", ""]]
        res = []
        for word in words:
            surface = word.split("\t")[0]
            if surface in self.contentword_dict:
                res.append(self.contentword_dict[surface])
        return res
    # randomize theta and phi
    def init_params(self):
        eps = 10**(-2)
        theta = L1_normalize([random.random()+eps for _ in range(self.K)])
        phi = []
        for k in range(self.K):
            phi.append(L1_normalize([random.random()+eps for _ in range(self.V)]))
        return theta, phi
    # generate a text from the trained model
    def generate(self):
        sum_theta = []
        buf = 0
        for t in self.theta:
            buf += t
            sum_theta.append(buf)
        k = bisect.bisect(sum_theta, random.random())
        sum_phi_k = []
        buf = 0
        for p in self.phi[k]:
            buf += p
            sum_phi_k.append(buf)
        res = []
        for n in range(10):
            res.append(bisect.bisect(sum_phi_k, random.random()))
        return [self.contentword_list[index] for index in res]
def L1_normalize(li):
    """Each value li[i] is supporsed to be greater than 0."""
    s = sum(li)
    return [l/s for l in li]

　以下のように実行することができ、二つのドキュメントを分離して学習できていることがわかります。

1
2
3
4
5
6
7
8
9
10
11
12
>>> texts = ["吾輩は猫である。名前はまだ無い。", "親譲りの無鉄砲で小供の時から損ばかりしている。"]
>>> umm = UnigramMixtureModel(texts, K=2)
>>> umm.generate()
['猫', '猫', '猫', '名前', '名前', '猫', '猫', '猫', '猫', '猫']
>>> umm.generate()
['損', '損', '無鉄砲', '親譲り', '無鉄砲', '親譲り', '損', '損', '親譲り', '損']
[/python]
>>> umm.theta
[0.5, 0.5]
>>> umm.phi
[[0.5, 0.5, 0.0, 0.0, 0.0],
 [0.0, 0.0, 0.3333333333333333, 0.3333333333333333, 0.3333333333333333]]

まとめ

  • 混合ユニグラムモデルについて説明しました
  • 混合ユニグラムモデルとEMアルゴリズムを実装しました

参考文献

  • 岩田具治『トピックモデル』
    • 混合ユニグラムモデル、LDAについての解説あり
    • EMアルゴリズムについての解説あり
  • 佐藤一誠『トピックモデルによる統計的潜在意味解析』
    • LDAについての解あり
    • グラフィカルモデルについての解説あり
  • 井手剛『入門 機械学習による異常検知』
    • EMアルゴリズムについての解説あり
  • 山西健司『データマイニングによる異常検知』
    • EMアルゴリズムについての解説あり

テックブログ新着情報のほか、AWSやGoogle Cloudに関するお役立ち情報を配信中！

tmtk

データ分析と機械学習とソフトウェア開発をしています。 アルゴリズムとデータ構造が好きです。

Recommends

こちらもおすすめ

Special Topics

注目記事はこちら

これから始めるBigQuery基礎知識

データ分析入門
これから始めるBigQuery基礎知識

2024.02.28

ホワイトペーパー

AWSの請求代行リセールサービス

　AWSの料金が 10 %割引になる！
『AWSの請求代行リセールサービス』

2024.07.16

サービス