VAEを用いたUNIXセッションのなりすまし検出
こんにちは。データサイエンスチームの t2sy です。
この記事は NHN テコラス Advent Calendar 2018 の17日目の記事です。
はじめに
ニューラルネットワークを用いた代表的な生成モデルとして VAE (Variational Autoencoder) と GAN (Generative Adversarial Network) の2つが知られています。生成モデルは異常検知にも適用できます。今回は、VAE を用いたUNIXセッションのなりすまし検出を試してみたのでご紹介します。
- VAEと異常検知
- データセット
- fastTextによるUNIXコマンドの分散表現
- KerasでVAE
実行環境は以下です。
- Amazon EC2 p2.xlarge インスタンス
- Ubuntu 16.04
- Python 3.4.5
- Keras 2.1.6
- TensorFlow 1.8.0
VAEと異常検知
VAE (Kingma, 2013; Rezende et al., 2014) は近似推論を用いた勾配に基づく方法で訓練できる生成モデルです。
VAE はエンコーダとデコーダで構成されますが、AE (Autoencoder) と異なり、エンコーダは観測データ X について潜在変数 z を生成する確率分布のパラメータに変換します。基本となる正規分布の場合は平均と分散です。エンコーダ は観測データ X が与えられた基で潜在変数 z を推論します。一方、デコーダ
は潜在変数 z から観測データ X を復元しようとします。
VAE はエンコーダとデコーダのパラメータについて生成されるデータに関する変分下界 (evidence lower bound; ELBO) を最大化することによって訓練されます。また、確率的勾配法を適用可能とするため確率的勾配変分ベイズ (stochastic gradient variational bayes; SGVB) という技法が使われます。
生成モデルは訓練データの確率分布を反映しており、確率分布から現れにくいパターンは異常と解釈することで異常検知に応用することができます。VAE による異常検知は画像や動画、時系列データ解析などに応用されています。[1, 2, 3]
異常の判定方法は、単純に VAE の再構成誤差 (reconstruction error) が閾値より大きい場合に異常と判定する方法や、再構成誤差に基づく異常スコアを定義し用いる方法、再構成確率 (reconstruction probability) が閾値より低い場合に異常と判定する方法などがあります。[4]
データセット
今回、実験で用いるデータセットは Masquerading User Data です。SEA (Schonlau et al.) データセットとも呼ばれるようです。
70人のUNIXコマンド列が含まれ、各ユーザは15,000コマンドからなります。User1 の最初の10コマンドは以下となります。
$ head MasqueradeDat/User1 cpp sh xrdb cpp sh xrdb mkpts env csh csh
ユーザ70人は50人の通常ユーザと20人のなりすましユーザの2つのクラスに分けられます。通常ユーザ50人の前半5,000コマンドには、なりすましは含まれません。後半10,000コマンドは100コマンドからなる100セッションに分けられており、セッションごとに1%の確率でなりすましが発生し、80%の確率で次のセッションでもなりすましが継続するように生成されています。
なりすましか否かのラベルは masquerade_summary.txt に書かれています。このファイルは100行50列で各列はユーザ、各行は後半10,000コマンドの100セッションに対応しています。値が0の場合は通常ユーザ、1の場合はなりすましユーザを表します。
fastTextによるコマンドの分散表現
fastText (Armand Joulin et al., 2016) を用いてUNIXコマンドの分散表現を獲得してみます。
まず、なりすましを含まない各ユーザの前半5,000コマンドをスペースで区切ってから連結し、ユーザごとの文を作り保存します。次に、fastText.train_unsupervised() で保存したファイルを指定し訓練します。今回は Skip-Gram モデルとしました。
import fastText
model = fastText.train_unsupervised("UserALL_train.txt", "skipgram", dim=50, minCount=1)
得られたコマンドの分散表現を UMAP (Uniform Manifold Approximation and Projection) (Leland McInnes et al., 2018) で可視化します。UMAP は多様体学習による次元削減手法で、 t-SNE と同程度の可視化の品質を持ちつつも高速に動作する手法です。
import umap
embedding = umap.UMAP(n_neighbors=15,
metric='correlation').fit_transform(unique_commands.iloc[:,1:51])
結果を図示します。全636コマンドを表示すると見えづらくなるため、出現回数が多い200コマンドを表示します。
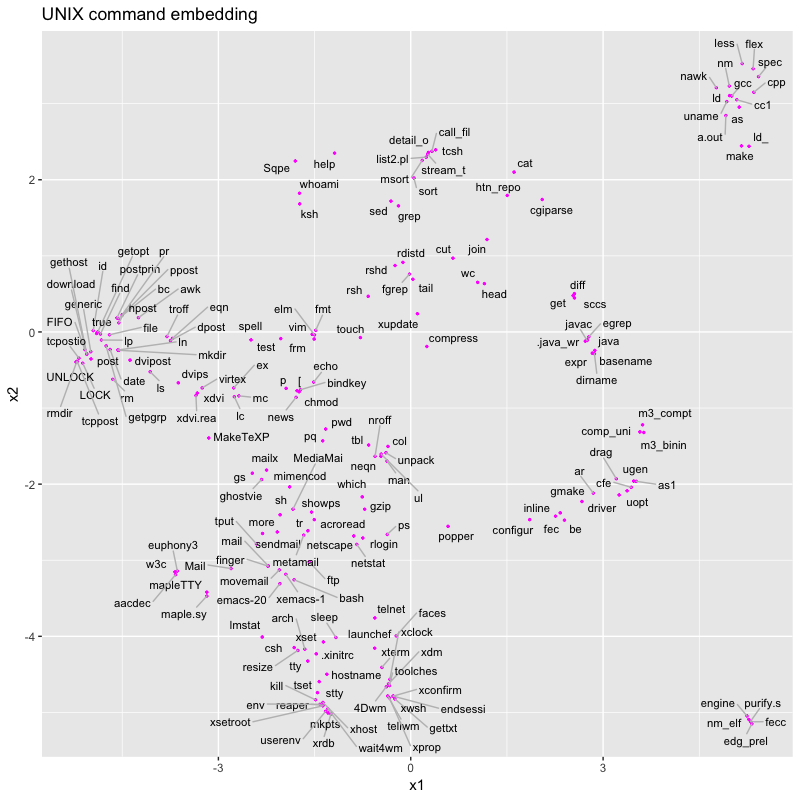
mail、Mail、metamail、sendmail、movemail などのメールに関するコマンドが中央やや左下に集まっていることが確認できます。また、make、gcc、flex などのコマンドが右上の離れたところに集まっているのも面白いです。
KerasでVAE
例として、User2 のコマンド列を学習してみます。最初に User2 のコマンド列 (前半5,000コマンド) から fastText で分散表現を得ます。
次に Keras で VAE を実装します。
今回扱うデータは系列データなので、まず1次元畳み込みニューラルネットワーク (1D CNN) や LSTM を試したのですが、思うような結果が得られませんでした。特に LSTM ではメモリ負荷が大きく手軽に実験したい場合には向いていない印象でした。
2次元畳み込みニューラルネットワーク (2D CNN) で多少良い結果が得られたため 2D CNN の結果を示します。
import numpy as np
from keras import layers
from keras import backend as K
from keras.models import Model
from keras.layers.core import Lambda
from keras.optimizers import Adam
K.clear_session()
shape = (100, 50, 1)
epochs = 12
batch_size = 16
latent_dim = 2
input_cmd = keras.Input(shape=shape)
x = layers.Conv2D(32, 3,
padding='same', activation='relu')(input_cmd)
x = layers.Conv2D(64, 3,
padding='same', activation='relu',
strides=(2, 2))(x)
x = layers.Dropout(0.1)(x)
x = layers.Conv2D(64, 3,
padding='same', activation='relu')(x)
x = layers.Dropout(0.2)(x)
x = layers.Conv2D(64, 3,
padding='same', activation='relu')(x)
x = layers.Dropout(0.2)(x)
shape_before_flattening = K.int_shape(x)
x = layers.Flatten()(x)
x = layers.Dense(32, activation='relu')(x)
z_mean = layers.Dense(latent_dim)(x)
z_log_var = layers.Dense(latent_dim)(x)
def sampling(args):
z_mean, z_log_var = args
epsilon = K.random_normal(shape=(K.shape(z_mean)[0], latent_dim),
mean=0., stddev=1.)
return z_mean + K.exp(z_log_var) * epsilon
z = Lambda(sampling)([z_mean, z_log_var])
decoder_input = layers.Input(K.int_shape(z)[1:])
x = layers.Dense(np.prod(shape_before_flattening[1:]),
activation='relu')(decoder_input)
x = layers.Reshape(shape_before_flattening[1:])(x)
x = layers.Conv2DTranspose(32, 3, strides=(2, 2),
padding='same', activation='relu')(x)
x = layers.Conv2D(1, 3,
padding='same', activation='sigmoid')(x)
decoder = Model(decoder_input, x)
z_decoded = decoder(z)
class CustomVariationalLayer(keras.layers.Layer):
def vae_loss(self, x, z_decoded):
x = K.flatten(x)
z_decoded = K.flatten(z_decoded)
xent_loss = keras.metrics.binary_crossentropy(x, z_decoded)
kl_loss = -5e-4 * K.mean(
1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
return K.mean(xent_loss + kl_loss)
def call(self, inputs):
x = inputs[0]
z_decoded = inputs[1]
loss = self.vae_loss(x, z_decoded)
self.add_loss(loss, inputs=inputs)
return x
y = CustomVariationalLayer()([input_cmd, z_decoded])
モデルをコンパイルします。
vae = Model(input_cmd, y) vae.compile(optimizer=Adam(), loss=None) vae.summary()
モデルのネットワークを確認します。
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_1 (InputLayer) (None, 100, 50, 1) 0
__________________________________________________________________________________________________
conv2d_1 (Conv2D) (None, 100, 50, 32) 320 input_1[0][0]
__________________________________________________________________________________________________
conv2d_2 (Conv2D) (None, 50, 25, 64) 18496 conv2d_1[0][0]
__________________________________________________________________________________________________
dropout_1 (Dropout) (None, 50, 25, 64) 0 conv2d_2[0][0]
__________________________________________________________________________________________________
conv2d_3 (Conv2D) (None, 50, 25, 64) 36928 dropout_1[0][0]
__________________________________________________________________________________________________
dropout_2 (Dropout) (None, 50, 25, 64) 0 conv2d_3[0][0]
__________________________________________________________________________________________________
conv2d_4 (Conv2D) (None, 50, 25, 64) 36928 dropout_2[0][0]
__________________________________________________________________________________________________
dropout_3 (Dropout) (None, 50, 25, 64) 0 conv2d_4[0][0]
__________________________________________________________________________________________________
flatten_1 (Flatten) (None, 80000) 0 dropout_3[0][0]
__________________________________________________________________________________________________
dense_1 (Dense) (None, 32) 2560032 flatten_1[0][0]
__________________________________________________________________________________________________
dense_2 (Dense) (None, 2) 66 dense_1[0][0]
__________________________________________________________________________________________________
dense_3 (Dense) (None, 2) 66 dense_1[0][0]
__________________________________________________________________________________________________
lambda_1 (Lambda) (None, 2) 0 dense_2[0][0]
dense_3[0][0]
__________________________________________________________________________________________________
model_1 (Model) (None, 100, 50, 1) 258753 lambda_1[0][0]
__________________________________________________________________________________________________
custom_variational_layer_2 (Cus [(None, 100, 50, 1), 0 input_1[0][0]
model_1[1][0]
==================================================================================================
Total params: 2,911,589
Trainable params: 2,911,589
Non-trainable params: 0
__________________________________________________________________________________________________
モデルを訓練します。訓練で使うのは、なりすましを含まない前半5,000コマンドです。
history = vae.fit(x=train_X_w[:4000], y=None,
shuffle=True,
epochs=epochs,
batch_size=batch_size,
validation_data=(train_X_w[4000:], None))
エポックごとの訓練損失と検証損失は以下のようになりました。
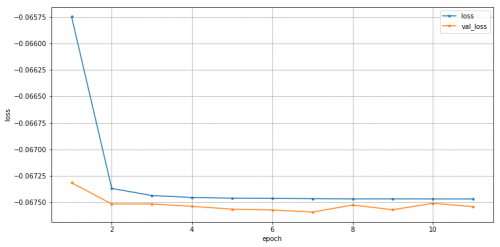
次に、訓練されたモデルを用いて、テストデータ (なりすましを含む後半10,000コマンド) の損失を計算します。User2 ではテストデータ中の11,001コマンドから11,300コマンドまでの3セッションでなりすましが発生しています。
11001 generic 11002 generic 11003 date 11004 generic 11005 gethost 11006 download 11007 tcpostio 11008 tcpostio 11009 tcpostio 11010 tcpostio ... 11291 as 11292 gcc 11293 gcc 11294 uname 11295 nawk 11296 ld_ 11297 nm 11298 ld 11299 gcc 11300 gcc
テストデータに含まれる未知語は前半5,000コマンド中で出現頻度が低いコマンドのベクトルを平均化しています。
未知語を意図的に極端な値を持つベクトルとすることで True Positive (TP) は増えることが予想されますが、新しいコマンドを使う度に異常検知され易くなり同時に False Positive (FP) も増えることが考えられます。結果として、Recall は上昇する一方で Precision は下降する懸念があるため、この方法は避けました。
損失の推移は以下となりました。背景が薄い赤色のエリアがなりすましが発生している部分です。なりすまし部分で損失が大きくなっていることが確認できます。
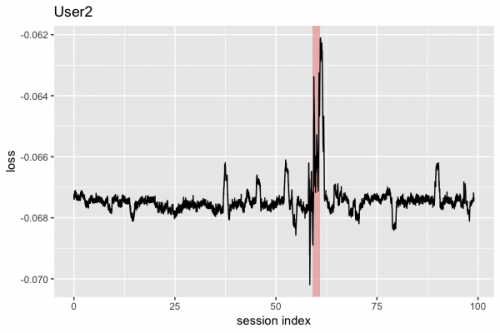
続いて、VAEがUNIXコマンド列を上手く復元できているか確認します。近似的に復元されたベクトルから fastText を使い最も類似しているコマンドを取り出します。テストデータの最初の20コマンドを確認してみます。この部分の損失は -0.06736 です。
| No. | 観測コマンド | 生成されたコマンド |
|---|---|---|
| 5001 | flex | flex |
| 5002 | uname | uname |
| 5003 | nawk | nawk |
| 5004 | cpp | cpp |
| 5005 | cc1 | cc1 |
| 5006 | as | as |
| 5007 | gcc | gcc |
| 5008 | gcc | gcc |
| 5009 | uname | uname |
| 5010 | nawk | nawk |
| 5011 | cpp | cpp |
| 5012 | cc1 | cc1 |
| 5013 | gcc | gcc |
| 5014 | gcc | gcc |
| 5015 | make | make |
| 5016 | bison | bison |
| 5017 | flex | flex |
| 5018 | uname | uname |
| 5019 | nawk | nawk |
| 5020 | cpp | cpp |
最初の20コマンドでは、なりすましが発生していないため上手く復元できていることが確認できます。
次に損失が -0.06210 と比較的大きい部分を見てみます。
| No. | 観測コマンド | 生成されたコマンド |
|---|---|---|
| 11104 | LOCK | LOCK |
| 11105 | movemail | sendmail |
| 11106 | movemail | sendmail |
| 11107 | netscape | neqn |
| 11108 | netscape | neqn |
| 11109 | netscape | neqn |
| 11110 | netscape | neqn |
| 11111 | netscape | neqn |
| 11112 | sendmail | sendmail |
| 11113 | sendmail | sendmail |
| 11114 | sendmail | sendmail |
| 11115 | movemail | sendmail |
| 11116 | movemail | sendmail |
| 11117 | movemail | sendmail |
| 11118 | sendmail | sendmail |
| 11119 | sendmail | sendmail |
| 11120 | sendmail | sendmail |
| 11121 | movemail | sendmail |
| 11122 | movemail | sendmail |
| 11123 | movemail | sendmail |
この部分ではなりすましが発生し、テストデータにしか含まれない netscape、movemail が使われているため、損失が大きくなっていることが窺えます。一方、movemail に対し sendmail という比較的似ているコマンドが生成されています。これはデコーダが近似的に復元したベクトルが fastText による埋め込み空間上で最も似ている既知のコマンドとして sendmail が選ばれたということで興味深い点です。
おわりに
この記事では、VAEを用いたUNIXセッションのなりすまし検出についてご紹介しました。
今後の展望として、日々のコマンド履歴からデータセットを作り生成モデルを訓練させ、リアルタイム検出 (コマンド実行前にフックし推論) してみたいです。コマンドのオプションをどう扱うかなど工夫の余地は多そうなので、機会がありましたら記事にしたいと思います。
参考文献
- Anomaly Detection for Skin Disease Images Using Variational Autoencoder
- An overview of deep learning based methods for unsupervised and semi-supervised anomaly detection in videos
- Unsupervised Anomaly Detection via Variational Auto-Encoder for Seasonal KPIs in Web Applications
- Variational Autoencoder based Anomaly Detection using Reconstruction Probability
- A Recurrent Latent Variable Model for Sequential Data
- Deep Learning. An MIT Press book. (2015)
- Deep Learning with Python
テックブログ新着情報のほか、AWSやGoogle Cloudに関するお役立ち情報を配信中!
Follow @twitter2016年11月、データサイエンティストとして中途入社。時系列分析や異常検知、情報推薦に特に興味があります。クロスバイク、映画鑑賞、猫が好き。
Recommends
こちらもおすすめ
-

配色はセンスじゃなく理論でなんとかなる!②活用編
2018.12.15
-

社内エンジニア読書会の進め方 ーAI・機械学習チーム編ー
2019.4.4
-

子どもの寝かしつけが少し楽になる!スマートおばけの作り方
2018.12.3
-

機械学習 曲線フィッテングについて おまけ?編
2016.4.28
Special Topics
注目記事はこちら

データ分析入門
これから始めるBigQuery基礎知識
2024.02.28

AWSの料金が 10 %割引になる!
『AWSの請求代行リセールサービス』
2024.07.16


