最小二乗法とは?平均との関係を解説
こんにちは。データサイエンスチーム tmtkです。
この記事では、最小二乗法と平均の関係について説明します。最小二乗法は標準的には回帰分析で用いられますが、実は平均も最小二乗法で捉えることができます。
また、最小二乗法と平均の間と同じ関係が、“最小一乗法”と中央値の間にもあることを説明します。
最小二乗法と回帰
最小二乗法とは、回帰分析のパラメータとして、残差の二乗和を最小にするパラメータを選択する手法です。
線形回帰を例にとって具体的に説明します。線形回帰とは、
1. データが与えられている。
2. 変数の関係が
で近似できると仮定する。
3. の残差
の二乗和
を最小にする
を計算する。(これが 最小二乗法 )
4. 3. で得られたを用いて、データ列に
の関係があると見積もる。
という手続きです。
このような、回帰の手続きのうち、残差の二乗和を最小化する手順のことを、最小二乗法といいます。
AWSのビッグデータ活用・機械学習導入支援サービス
最小二乗法と算術平均
データが与えられているとします。
いま、距離の二乗和関数を最小にする
を求める問題を考えてみます。これは、二乗和を最小にする問題なので、ある意味で“最小二乗法”だと考えることができます。
を計算しましょう。
したがって、二次関数の一般論から、を最小にする
は
であることがわかります。これは
の算術平均です。
したがって、算術平均は“最小二乗法”で計算できると考えることができます。これで、最小二乗法と算術平均の意外な関係が明らかになりました。
【事例集】AIや機械学習によるビッグデータ活用をしたい方にオススメ!

「AIによるキャスト評価システムの構築」「データ分析基盤の運用費用9割削減」など、AWSを利用したAI、機械学習の成功事例をご紹介します。
“最小一乗法”と中央値
実は、最小二乗法と算術平均の間の関係が、“最小一乗法”と中央値の間にもあてはまることがわかります。以下で、これを説明します。なお、残差のL1ノルムの和の最小化をする方法はよく最小絶対値法などと呼ばれていますが、ここでは最小二乗法との対比を強調して“最小一乗法”と呼ぶことにします。
まず、中央値の定義を復習します。
定義. 中央値
- データの数が奇数個の場合。
データが与えられているとする。いま、データは昇順にならんでいるとする。すなわち、
が成り立っているとする。
このとき、このデータの中央値を
で定義する。 - データの数が偶数個の場合。
データが与えられているとする。いま、データは昇順にならんでいるとする。すなわち、
が成り立っているとする。
このとき、このデータの中央値を
で定義する。
さて、前の議論を、“最小一乗法”に変えて実行してみましょう。すると、次の定理が成り立ちます。
定理.
が
を満たしているとする。
関数を
で定義する。
このとき、の中央値は、
の最小値を与える。
証明の方針.
正確な証明を与える前に、証明の方針を述べます。
簡単な例として、が
の場合を考えてみます。
このとき、中央値は3です。
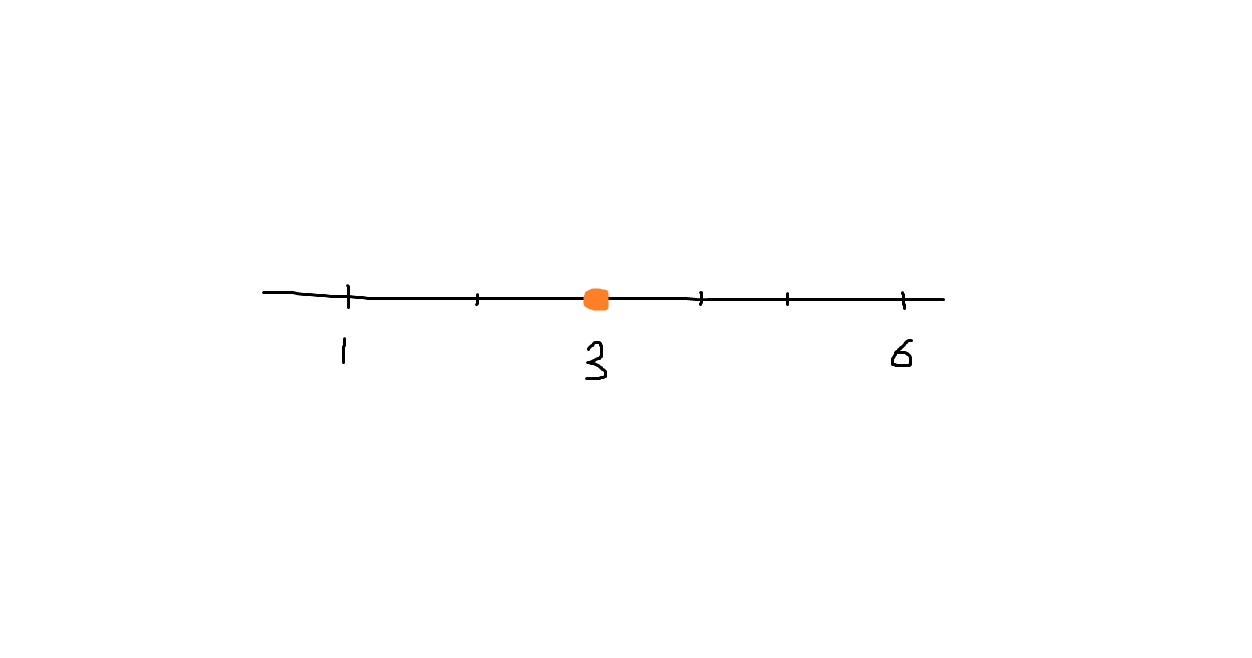
は、各点
から
の距離の和だと考えることができます。
定理の主張は、この距離の和がで最小になるということです。
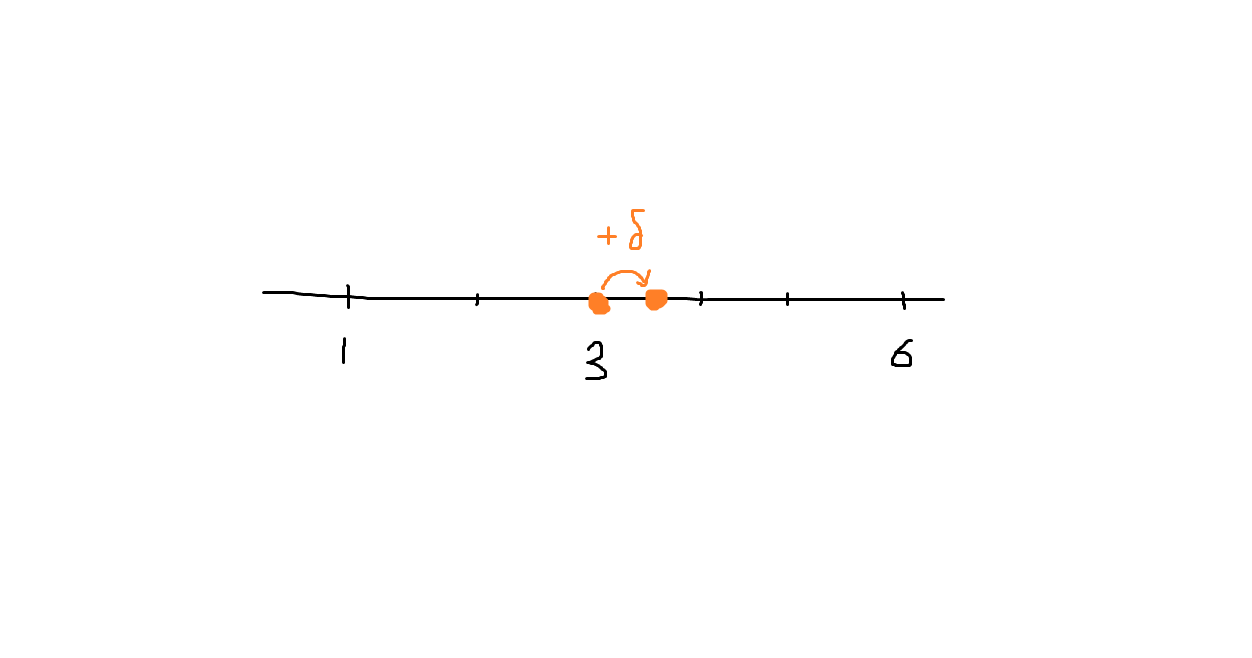
いま、はじめにあった
が、小さい距離
だけ増え、
になったとします。
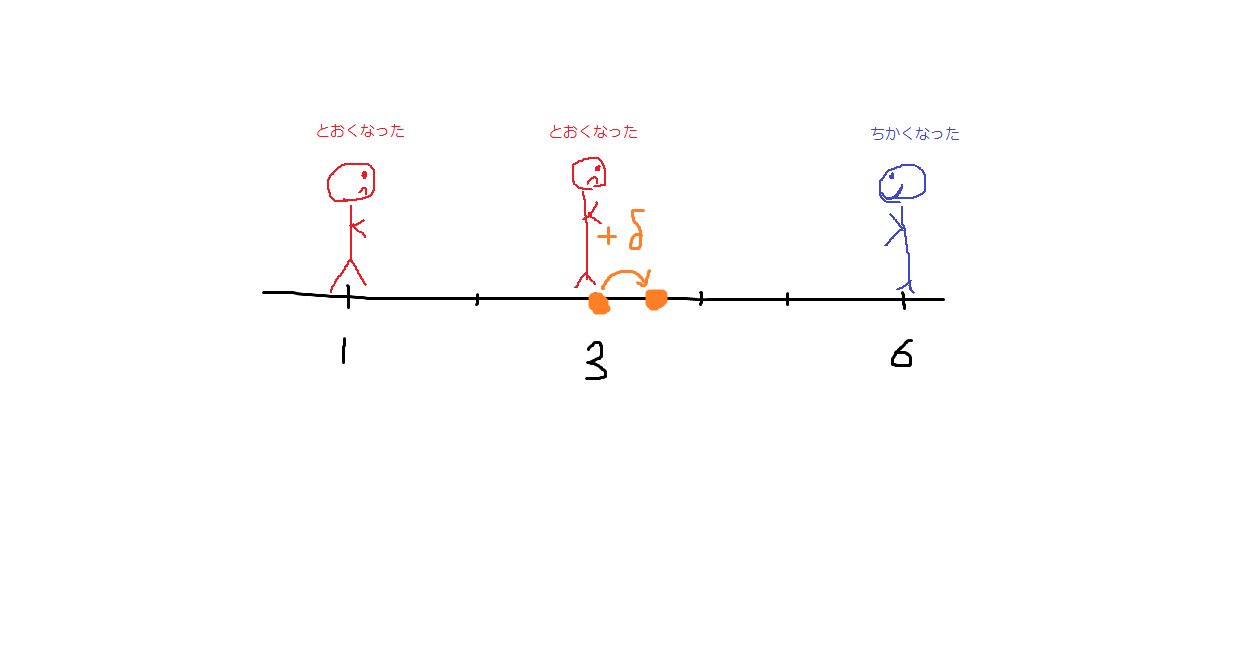
このとき、
から
の距離は、
から
に変化し、
だけ増える。
から
の距離は、
から
に変化し、
だけ増える。
から
の距離は、
から
に変化し、
だけ減る。
ということで、
これらを合計したは、
だけ増える。
ということがわかります。
これを一般化すると、おおざっぱに言って、
数直線上でが右に動くと、
より左側にあった点の数に比例して距離の和
が大きくなり、
より右側にあった点の数に比例して
が小さくなる。
が左に動くと、
より左側にあった点の数に比例して距離の和
が小さくなり、
より右側にあった点の数に比例して
が大きくなる。
ということがいえます。したがって、数直線上での左側にも右側にも同じ数の点がある状態が、
が一番小さくなる状態であり、そのような
は中央値です。
この描像に沿って、証明をします。
証明.
データの数が偶数の場合も同様なので、奇数の場合にだけ証明する。
とおく。いま、
が成り立っている。
が
の最小値を与えることを証明するためには、任意の
に対して
が成立することを示せばよい。
を任意にとり、
とおく。
のとき。
に対して、
が成り立つ。
また、に対して、三角不等式より
が成り立つ。したがって、
が成り立つ。
以上より、となって、
が成立する。
のとき。
- の場合と同様。
以上より、定理が成立することがわかる。
まとめ
差の二乗和を最小化するのが算術平均であり、差の絶対値の和を最小化するのが中央値です。
参考
倉田博史・星野崇宏『入門統計解析』新世社,2009年
インフラ担当者の業務負荷を軽減!AWS運用の自動化機能とは?

AWSにはシステム運用を自動化できるサービスが多数取り揃えられており、本資料では、これら機能の概要をわかりやすく解説します。
テックブログ新着情報のほか、AWSやGoogle Cloudに関するお役立ち情報を配信中!
Follow @twitterデータ分析と機械学習とソフトウェア開発をしています。 アルゴリズムとデータ構造が好きです。
Recommends
こちらもおすすめ
-

機械学習を学ぶための準備 その5(行列のいろいろ)
2015.12.19
-

新卒 IoT 女子、自称やめるってよ
2016.7.20
-

gulp+babelでのフロントエンド開発について – 2. gulpによるビルド
2015.11.17
-

Terraform AWS Moduleのすすめ
2022.5.25
-

Oktaがあるとすごく助かる人たちってどんな人たち?
2024.2.29
-

こんにちは Okta
2024.2.13
Special Topics
注目記事はこちら

データ分析入門
これから始めるBigQuery基礎知識
2024.02.28

AWSの料金が 10 %割引になる!
『AWSの請求代行リセールサービス』
2024.07.16

