ディープラーニングにおけるdeconvolutionとは何か

tmtk

2018.11.6

Topics

deconvolution, transpose convolution, fractionally-strided convolution, up-convolution, backwards convolutionはすべておなじもの
convolutionとは何か
deconvolutionとは何か
数学的な注意
まとめ
参考文献

　こんにちは。データサイエンスチームのtmtkです。
　この記事では、GAN（Generative Adversarial Network）やautoencoderの文献でよく出てくる、deconvolutionというものについて解説します。

deconvolution, transpose convolution, fractionally-strided convolution, up-convolution, backwards convolutionはすべておなじもの

　GANやautoencoderの文献を読んでいると、deconvolutionやup-convolutionなどという単語に出会うことがあります。他にも、transpose convolution、fractionally-strided convolution、backwards convolutionなど、似た単語がいろいろ出てきます。
　しかし、私の理解では、これらはすべて同じものを指す単語です。
　以下で、実際にこれらの単語が出てくるところを例示します。DCGANの論文では、

fractionally-strided convolutions (in some recent papers, these are wrongly called deconvolutions)
（fractinally-strided convlution（最近の論文では、間違ってdeconvolutionと呼ばれていることがある））

と書かれています。Fully Convolutional Networks for Semantic Segmentationという論文では、

backwards convolution (sometimes called deconvolution)
（backwards convolution（deconvolutionと呼ばれることもある））

と書かれています。Troubling Trends in Machine Learning Scholarship（学問としての機械学習の厄介な動向）という論文では、

3.4.2 Overloading Technical Terminology
A second avenue of misuse consists of taking a term that holds precise technical meaning and using it in an imprecise or contradictory way. Consider the case of deconvolution, which formally describes the process of reversing a convolution, but is now used in the deep learning literature to refer to transpose convolutions (also called up-convolutions) as commonly found in auto-encoders and generative adversarial networks.

として、「deconvolutionは形式的にはconvolutionの逆という意味だが、現在では単にtranspose convolution（up-convolutionとも呼ばれる）のことを指してしまっている」という指摘がされています。（この論文によれば、Deconvolutional networksという論文では、deconvolutionという単語が本来のとおりconvolutionの逆の操作を指しているそうです。deconvolutionがほかと違った意味をもつ少ない例の一つかもしれません。）
　このように、いろいろな呼ばれ方をしていますが、基本的には同じものを指しています。以下では、これらすべてをdeconvolutionと統一して呼ぶことにします。

convolutionとは何か

　deconvolutionの解説をしたいのですが、その前に、機械学習におけるconvolution（畳み込み）について復習します。機械学習分野でいうconvolutionは、数学などでいうconvolutionとは若干違ったものになっているので、注意が必要です。
　以前の記事でも説明しましたが、convolutionは次のような操作です。例を挙げて説明します。入力が長さ6のベクトル

$x = (x_1, \dots, x_6)$
、convolutionのフィルターが長さ2のベクトル
$a = (a_1, a_2)$
のとき、入力 $x$ のフィルター $a$ によるconvolutionは長さ5のベクトル
$(a_1x_1+a_2x_2, a_1x_2+a_2x_3, a_1x_3+a_2x_4, a_1x_4+a_2x_5, a_1x_5+a_2x_6)$
になります。

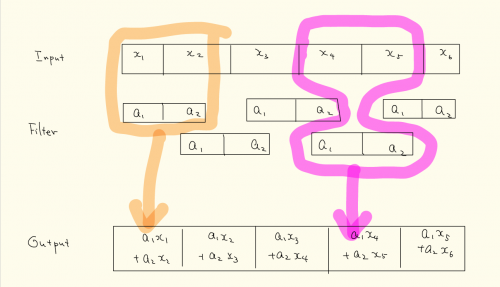
上の例はstrideという値が1の場合のconvolutionで、strideを2に変更すると、convolutionは長さ3のベクトル $(a_1x_1 + a_2x_2, a_1x_3 + a_2x_4, a_1x_5+a_2x_6)$ になり、長さが短くなります。

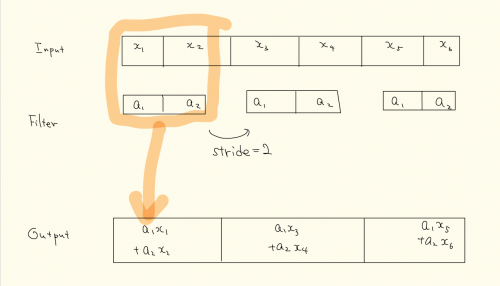
　ここで、convolutionは線形写像であり、行列で表示できることに注意します。上のstrideが2の場合の例で考えると、

$\left(\begin{array}{c}a_1x_1+a_2x_2\\a_1x_3+a_2x_4\\a_1x_5+a_2x_6\end{array}\right) = \left(\begin{array}{cccccc}a_1 & a_2 & 0& 0& 0& 0\\ 0&0&a_1&a_2&0&0\\ 0&0&0&0&a_1&a_2 \end{array}\right)\left(\begin{array}{c}x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6\end{array}\right)$
という式が成り立つので、convolutionは入力の縦ベクトル $x^\intercal$ に行列
$A = \left(\begin{array}{cccccc}a_1 & a_2 & 0& 0& 0& 0\\ 0&0&a_1&a_2&0&0\\ 0&0&0&0&a_1&a_2 \end{array}\right)$
を左からかけることだと考えることができます。
　ここでは1次元データの場合について考察しましたが、画像などの2次元データの場合にも全く同様に考えることができます。たとえば、縦が224pixel、横が224pixelの2次元データは、長さ224×224の1次元データだと思えば、やはりconvolutionを線形写像として書き下すことができます。

deconvolutionとは何か

　deconvolutionについて説明します。
　convolutionでは、strideが1より大きいと、入力の次元より出力の次元が小さくなってしまいます。deconvolutionはこの点でconvolutionの逆の操作だとみなすことができ、入力より次元が大きい出力を得ることができます。また、convolutionをしてから、そのconvolutionに「対応する」deconvolutionをすれば、convolutionをする前の入力と同じ次元の出力をdeconvolutionから得ることができます。
　deconvolutionは、数学的に端的にいってしまえば、convolutionに対応する行列の転置（transpose）を左からかける操作です。
　上で考察した例では、入力が次元6のベクトル $x = (x_1, \dots, x_6)$ 、convolutionのフィルターが次元が2のベクトル $a = (a_1, a_2)$ 、strideが2のとき、convolutionに対応する行列は

$A = \left(\begin{array}{cccccc}a_1 & a_2 & 0& 0& 0& 0\\ 0&0&a_1&a_2&0&0\\ 0&0&0&0&a_1&a_2 \end{array}\right)$

なのでした。それに対応するdeconvolutionは、入力が次元2のベクトル $y = (y_1, y_2, y_3)$ 、deconvolutionのフィルターが次元2のベクトル $a = (a_1, a_2)$ 、strideが2のときのdeconvolutionで、それはconvolutionをに対応する行列 $A$ の転置行列

$A^\intercal = \left(\begin{array}{cccccc}a_1 & a_2 & 0& 0& 0& 0\\ 0&0&a_1&a_2&0&0\\ 0&0&0&0&a_1&a_2 \end{array}\right) ^\intercal = \left(\begin{array}{ccc} a_1 & 0 & 0\\a_2&0&0\\0&a_1&0\\0&a_2&0\\0&0&a_1\\0&0&a_2\end{array}\right)$

を $y^\intercal$ に左からかけて、

$A^\intercal \left(\begin{array}{c}y_1 \\y_2\\y_3\end{array}\right) = \left(\begin{array}{c} a_1y_1\\a_2y_1\\a_1y_2\\a_2y_2\\a_1y_3\\a_2y_3\end{array}\right)$

となります。

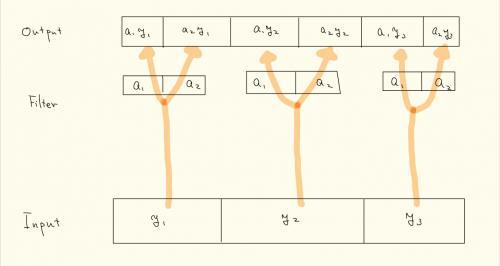
convolutionでは長さ6のデータが長さ2に縮小されましたが、deconvolutionで長さ2のデータが元の長さ6に拡大されている様子がわかると思います。

　ここでは1次元のデータについて解説しましたが、convolutionのときと同じように、2次元以上のデータに対してもまったく同じように考えることができます。

数学的な注意

　線形写像 $f\colon k^n \to k^m$ を標準基底 $\{e_1, \dots, e_n\}, \{e_1, \dots, e_m\}$ で表示した行列が $A = (a_{ij})$ のとき、その双対写像 $f^*\colon (k^m)^* \to (k^n)^*$ を双対基底 $\{e^1, \dots, e^m\}, \{e^1,\dots, e^n\}$ で表示した行列は $A^\intercal$ になります。双対写像が引き戻しであることを考えれば、convolutionで縮小されたデータがdeconvolutionが拡大される状況がわかりやすいかもしれません。

まとめ

　deconvolution, transpose convolution, fractionally-strided convolution, up-convolution, backwards convolutionはすべて同じ操作を指し、それはconvolutionをあらわす行列の転置行列であらわされる操作です。deconvolutionによってデータの長さが大きくなるので、生成ネットワークやautoencoderのdecoder部分で使われます。