相関係数は外れ値の影響をうけやすい？Pythonで確認してみた。

tmtk

Data Science

2018.2.28

Topics

相関係数
相関係数と外れ値
解釈
まとめ
参考

こんにちは。データサイエンスチーム tmtkです。
この記事では、外れ値が相関係数に与える影響を観察します。

相関係数

以前の記事で簡単に説明したように、相関係数（ピアソンの積率相関係数）は2つの変数の間にある線形関係の強弱を測る指標です。
諸説ありますが、相関係数の絶対値がおおむね0.7以上あれば強い相関があると判断されることが多いようです。

相関係数と外れ値

相関係数は外れ値の影響を強く受けます。これを確認します。
まず、Pythonで無相関のデータを作り出します。IPythonを起動し、数値計算ライブラリnumpyによって乱数を発生させます。

import numpy as np # numpyのimport
np.set_printoptions(suppress=True) # 指数表示を禁止
np.random.rand(0) # 乱数のseedを固定
x = np.random.rand(100)
y = np.random.rand(100)

これで、変数x, yに0以上1以下の乱数が100個ずつ入ります。

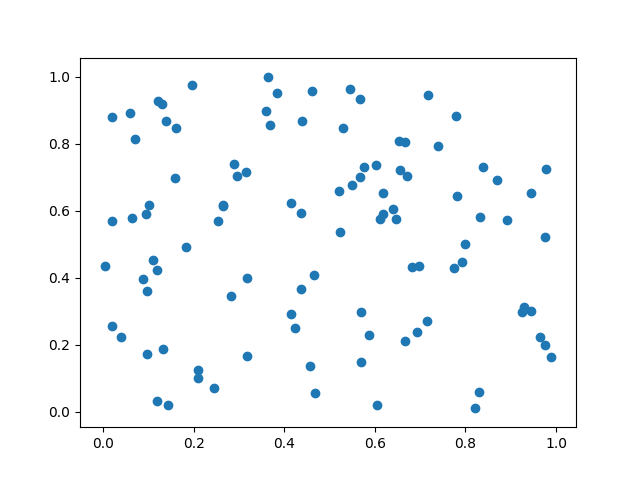
（Xとyの散布図）

In [8]: x
Out[8]:
array([ 0.5488135 ,  0.71518937,  0.60276338,  0.54488318,  0.4236548 ,
        0.64589411,  0.43758721,  0.891773  ,  0.96366276,  0.38344152,
        0.79172504,  0.52889492,  0.56804456,  0.92559664,  0.07103606,
        0.0871293 ,  0.0202184 ,  0.83261985,  0.77815675,  0.87001215,
        0.97861834,  0.79915856,  0.46147936,  0.78052918,  0.11827443,
        0.63992102,  0.14335329,  0.94466892,  0.52184832,  0.41466194,
        0.26455561,  0.77423369,  0.45615033,  0.56843395,  0.0187898 ,
        0.6176355 ,  0.61209572,  0.616934  ,  0.94374808,  0.6818203 ,
        0.3595079 ,  0.43703195,  0.6976312 ,  0.06022547,  0.66676672,
        0.67063787,  0.21038256,  0.1289263 ,  0.31542835,  0.36371077,
        0.57019677,  0.43860151,  0.98837384,  0.10204481,  0.20887676,
        0.16130952,  0.65310833,  0.2532916 ,  0.46631077,  0.24442559,
        0.15896958,  0.11037514,  0.65632959,  0.13818295,  0.19658236,
        0.36872517,  0.82099323,  0.09710128,  0.83794491,  0.09609841,
        0.97645947,  0.4686512 ,  0.97676109,  0.60484552,  0.73926358,
        0.03918779,  0.28280696,  0.12019656,  0.2961402 ,  0.11872772,
        0.31798318,  0.41426299,  0.0641475 ,  0.69247212,  0.56660145,
        0.26538949,  0.52324805,  0.09394051,  0.5759465 ,  0.9292962 ,
        0.31856895,  0.66741038,  0.13179786,  0.7163272 ,  0.28940609,
        0.18319136,  0.58651293,  0.02010755,  0.82894003,  0.00469548])

In [9]: y
Out[9]:
array([ 0.67781654,  0.27000797,  0.73519402,  0.96218855,  0.24875314,
        0.57615733,  0.59204193,  0.57225191,  0.22308163,  0.95274901,
        0.44712538,  0.84640867,  0.69947928,  0.29743695,  0.81379782,
        0.39650574,  0.8811032 ,  0.58127287,  0.88173536,  0.69253159,
        0.72525428,  0.50132438,  0.95608363,  0.6439902 ,  0.42385505,
        0.60639321,  0.0191932 ,  0.30157482,  0.66017354,  0.29007761,
        0.61801543,  0.4287687 ,  0.13547406,  0.29828233,  0.56996491,
        0.59087276,  0.57432525,  0.65320082,  0.65210327,  0.43141844,
        0.8965466 ,  0.36756187,  0.43586493,  0.89192336,  0.80619399,
        0.70388858,  0.10022689,  0.91948261,  0.7142413 ,  0.99884701,
        0.1494483 ,  0.86812606,  0.16249293,  0.61555956,  0.12381998,
        0.84800823,  0.80731896,  0.56910074,  0.4071833 ,  0.069167  ,
        0.69742877,  0.45354268,  0.7220556 ,  0.86638233,  0.97552151,
        0.85580334,  0.01171408,  0.35997806,  0.72999056,  0.17162968,
        0.52103661,  0.05433799,  0.19999652,  0.01852179,  0.7936977 ,
        0.22392469,  0.34535168,  0.92808129,  0.7044144 ,  0.03183893,
        0.16469416,  0.6214784 ,  0.57722859,  0.23789282,  0.934214  ,
        0.61396596,  0.5356328 ,  0.58990998,  0.73012203,  0.311945  ,
        0.39822106,  0.20984375,  0.18619301,  0.94437239,  0.7395508 ,
        0.49045881,  0.22741463,  0.25435648,  0.05802916,  0.43441663])

このデータのxとyの相関係数を計算すると、-0.06610711となります。バラバラの乱数でデータを生成したので、0に近い相関係数が計算されています。これは自然な結果です。

In [10]: np.corrcoef(x, y)
Out[10]:
array([[ 1.        , -0.06610711],
       [-0.06610711,  1.        ]])

次に、このデータに外れ値 $(x, y) = (10, 10)$ を追加してみます。

x = np.concatenate([x, np.asarray([10])])
y = np.concatenate([y, np.asarray([10])])

これで、変数x, yそれぞれの末尾に値 $10$ が追加されました。
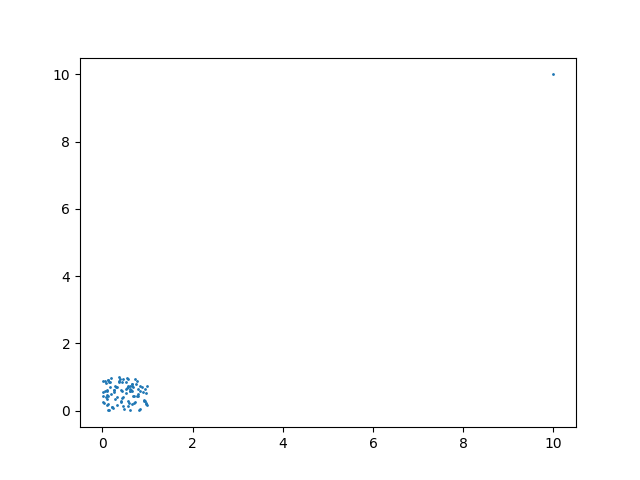
外れ値を加えたデータ
（外れ値を加えたXとyの散布図）

In [16]: x
Out[16]:
array([  0.5488135 ,   0.71518937,   0.60276338,   0.54488318,
         0.4236548 ,   0.64589411,   0.43758721,   0.891773  ,
         0.96366276,   0.38344152,   0.79172504,   0.52889492,
         0.56804456,   0.92559664,   0.07103606,   0.0871293 ,
         0.0202184 ,   0.83261985,   0.77815675,   0.87001215,
         0.97861834,   0.79915856,   0.46147936,   0.78052918,
         0.11827443,   0.63992102,   0.14335329,   0.94466892,
         0.52184832,   0.41466194,   0.26455561,   0.77423369,
         0.45615033,   0.56843395,   0.0187898 ,   0.6176355 ,
         0.61209572,   0.616934  ,   0.94374808,   0.6818203 ,
         0.3595079 ,   0.43703195,   0.6976312 ,   0.06022547,
         0.66676672,   0.67063787,   0.21038256,   0.1289263 ,
         0.31542835,   0.36371077,   0.57019677,   0.43860151,
         0.98837384,   0.10204481,   0.20887676,   0.16130952,
         0.65310833,   0.2532916 ,   0.46631077,   0.24442559,
         0.15896958,   0.11037514,   0.65632959,   0.13818295,
         0.19658236,   0.36872517,   0.82099323,   0.09710128,
         0.83794491,   0.09609841,   0.97645947,   0.4686512 ,
         0.97676109,   0.60484552,   0.73926358,   0.03918779,
         0.28280696,   0.12019656,   0.2961402 ,   0.11872772,
         0.31798318,   0.41426299,   0.0641475 ,   0.69247212,
         0.56660145,   0.26538949,   0.52324805,   0.09394051,
         0.5759465 ,   0.9292962 ,   0.31856895,   0.66741038,
         0.13179786,   0.7163272 ,   0.28940609,   0.18319136,
         0.58651293,   0.02010755,   0.82894003,   0.00469548,  10.        ])

（yについても同様）
今度はこの新しいxとyについての相関係数を計算してみましょう。

In [17]: np.corrcoef(x, y)
Out[17]:
array([[ 1.        ,  0.91257043],
       [ 0.91257043,  1.        ]])

今度は相関係数が0.91257043になっています。相関係数が0.9を超えており、これは通常強い相関関係があると判断される数値です。ランダムなデータに外れ値を一つ加えたことによって、無相関のデータが強い相関関係のあるデータに変わってしまいました。

解釈

もともと相関係数がほぼ0だったデータに対して、たった1つの外れ値を加えただけで、強い相関を示すデータになってしまいました。
今回の場合は人為的に作成したデータなので解釈が難しいところですが、例えばこの外れ値が測定機器の異常や入力ミスなどによる異常値だったとしたら、このデータに強い相関があると判断するのは明らかに間違いです。また、これが異常値ではない外れ値であったとしても、このような外れ値のある分布は「相関係数が0.9の分布」といわれて想像するデータの分布とはかなり違っているはずです。
データの様子を調べるときには、単純に相関係数などの数値的な指標を計算するだけではなく、可視化をするなどいろいろな角度からデータを分析したほうがよいです。